题目内容
下列函数中,在(0,+∞)既是增函数又是奇函数的是( )
| A、y=x+1 | ||
B、y=x+
| ||
C、y=x-
| ||
| D、y=x2+1 |
考点:函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用
分析:逐一分析四个答案中的四个函数的性质,然后和题目中的条件进行比照,即可得到答案.
解答:
解:A,函数y=x+1为非奇非偶函数,不满足条件;
B,y=x+
是奇函数,在(0,1)上单调递减,在(1,+∞)上单调递增,∴在(0,+∞)上不单调,故排除;
C,y=x-
=
,则有f(-x)=
=-
=-f(x),且f′(x)=
>0,故y=x-
在(0,+∞)既是增函数又是奇函数;
D,y=x2+1,因为f(-x)=(-x)2+1=x2+1=f(x),所以是偶函数,故排除.
故选:C.
B,y=x+
| 1 |
| x |
C,y=x-
| 1 |
| x |
| x2-1 |
| x |
| (-x)2-1 |
| -x |
| x2-1 |
| x |
| x2+1 |
| x2 |
| 1 |
| x |
D,y=x2+1,因为f(-x)=(-x)2+1=x2+1=f(x),所以是偶函数,故排除.
故选:C.
点评:本题考查的知识点是函数奇偶性与单调性的综合应用,其中熟练掌握基本初等函数的性质是解答本题的关键,属于基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=
,若f(x)≥ax恒成立,则a的取值范围是( )
|
A、(∞,
| ||||
B、[-
| ||||
C、[
| ||||
| D、[1,+∞) |
下列说法正确的是( )
| A、命题“?x∈R,ex>0”的否定是“?x∈R,ex<0” |
| B、命题“已知x,y∈R,若x+y≠10”,则x≠5或y≠5是真命题 |
| C、x2+2x≥ax在x∈[0,2]上恒成立?(x2+2x)min≥(ax)min在x∈[0,2]上恒成立” |
| D、命题:若a=-1,则函数f(x)=ax2+2x-1只有一个零点的逆命题为真命题 |
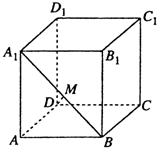 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.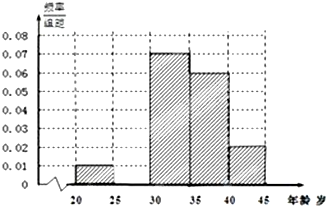 某市要对2000多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示.
某市要对2000多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示.