题目内容
3.(1)${({2x+\sqrt{x}})^5}$的展开式中,求x3的系数;(2)已知${({\sqrt{x}-\frac{a}{{\sqrt{x}}}})^5}$的展开式中含${x^{\frac{3}{2}}}$的项的系数为30,求a的值;
(3)$({x+\frac{a}{x}})•{({2x-\frac{1}{x}})^5}$的展开式中各项系数的和为2,求该展开式中的常数项.
分析 (1)在二项展开式的通项公式中,令x的幂指数等于3,求出r的值,即可求得展开式中x3的系数.
(2)根据所给的二项式,利用二项展开式的通项公式写出第r+1项,整理成最简形式,令x的指数为$\frac{3}{2}$求得r,再代入系数求出结果.
(3)根据$({x+\frac{a}{x}})•{({2x-\frac{1}{x}})^5}$的展开式中各项系数的和为2求得a=1,再根据它的展开式的通项公式求得它的常数项.
解答 解:(1)${({2x+\sqrt{x}})^5}$的展开式的通项公式为Tr+1=${C}_{5}^{r}$•${x}^{5-\frac{1}{2}r}$•25-r,
令5-$\frac{1}{2}r$=3,r=4,可得展开式中x3的系数为10;
(2)根据所给的二项式写出展开式的通项,Tr+1=$(-a)^{r}{C}_{5}^{r}{x}^{\frac{5}{2}-r}$
展开式中含${x^{\frac{3}{2}}}$的项的系数为30,
∴$\frac{5}{2}$-r=$\frac{3}{2}$,
∴r=1,并且-5a=30,解得a=-6;
(3)∵$({x+\frac{a}{x}})•{({2x-\frac{1}{x}})^5}$的展开式中各项系数的和为(a+1)(2-1)=2,
∴a=1,
(2x-$\frac{1}{x}$)5的通项为Tr+1=${C}_{5}^{r}•(-1)^{r}•{2}^{5-r}•{x}^{5-2r}$,
故常数项为${-C}_{5}^{3}•4$+${C}_{5}^{2}•8$=40.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
相关题目
13.设z=1-i(i是虚数单位),则$\frac{1}{z}$+$\overline{z}$=( )
| A. | $\frac{1}{2}-2i$ | B. | $\frac{3}{2}$+$\frac{3}{2}$i | C. | -$\frac{1}{2}$+2i | D. | $\frac{3}{2}$-$\frac{3}{2}$i |
15.一个几何体的三视图如图所示,则该几何体的表面积为( )
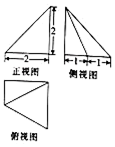

| A. | $12+\sqrt{3}$ | B. | $10+\sqrt{3}$ | C. | $10+2\sqrt{3}$ | D. | $11+\sqrt{3}$ |
13.已知复数z1=2-i,z2=1+i,其中i为虚数单位,设复数z=$\frac{{z}_{1}}{{z}_{2}}$,若a-z为纯虚数,则实数a的值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{1}{2}$ |