题目内容
8．i表示虚数单位，则1+i+i2+…+i2005=1+i．分析 由i+i2+i3+i4=0，再结合其周期性，解出即可．
解答 解：∵i+i2+i3+i4=i-1-i+1=0，
∴复数z=1+i+i2+i3+…+i2005=1+i，
故答案是：1+i．
点评 本题考查复数单位的乘方的意义，本题解题的关键是看出这些数字的和具有周期性，看出周期得到结果，本题是一个基础题．
练习册系列答案
相关题目
19．已知f（x）为定义在R行的可导函数，且f（x）＜f'（x）对于x∈R恒成立，且e为自然对数的底数，则下面正确的是（ ）
| A． | f（1）＞ef（0），f（2016）＞e2016f（0） | B． | f（1）＜ef（0），f（2016）＞e2016f（0） | ||
| C． | f（1）＞ef（0），f（2016）＜e2016f（0） | D． | f（1）＜ef（0），f（2016）＞e2016f（0） |
13．函数$y=\sqrt{2x+1}+ln（3-4x）$的定义域为（ ）
| A． | $（-\frac{1}{2}，\frac{3}{4}）$ | B． | $[-\frac{1}{2}，\frac{3}{4}]$ | C． | $（-∞，\frac{1}{2}]∪（\frac{3}{4}，+∞）$ | D． | $[-\frac{1}{2}，\frac{3}{4}）$ |
如图，四棱锥P-ABCD的底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点．
17．已知$\overrightarrow{a}$、$\overrightarrow{b}$为单位向量，|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{2}$|$\overrightarrow{a}-\overrightarrow{b}$|，则$\overrightarrow{a}$在$\overrightarrow{a}+\overrightarrow{b}$的投影为（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{2\sqrt{6}}{3}$ | C． | $\frac{2\sqrt{2}}{3}$ | D． | $\frac{\sqrt{6}}{3}$ |
18．若如图的程序框图运行的结构为S=-$\frac{1}{2}$，则判断框①中可以填入的是（ ）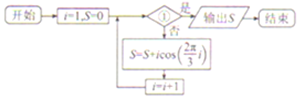
| A． | i＞4？ | B． | i≥4？ | C． | i＞3？ | D． | i≥3？ |