题目内容
△ABC的内角A,B,C的对边分别为a,b,c,且acosC+(c-2b)cosA=0.
(1)求∠A的大小;
(2)若△ABC的面积为2
且a=2
,求b+c的值.
(1)求∠A的大小;
(2)若△ABC的面积为2
| 3 |
| 3 |
考点:余弦定理,正弦定理
专题:解三角形
分析:(1)由正弦定理化简acosC+(c-2b)cosA=0,由两角和的正弦公式和诱导公式求出cosA,由内角的范围求出A;
(2)由三角形面积公式和题意求出bc,由余弦定理和整体代换求出b+c的值.
(2)由三角形面积公式和题意求出bc,由余弦定理和整体代换求出b+c的值.
解答:
解:(1)由题意知,acosC+(c-2b)cosA=0,
由正弦定理得,sinAcosC+(sinC-2sinB)cosA=0,
sinAcosC+sinCcosA-2sinBcosA=0,
则sin(A+C)-2sinBcosA=0,
由A+B+C=π得A+C=π-B,则sin(A+C)=sinB≠0代入上式得,
sinB-2sinBcosA=0,即cosA=
,
又0<A<π,则A=
;
(2)因为△ABC的面积为2
,所以
bcsinA=2
,则bc=8,
由余弦定理得,a2=b2+c2-2bccosA=(b+c)2-2bc-2bc×
,
则12=(b+c)2-3bc=(b+c)2-3×8,
解得b+c=6.
由正弦定理得,sinAcosC+(sinC-2sinB)cosA=0,
sinAcosC+sinCcosA-2sinBcosA=0,
则sin(A+C)-2sinBcosA=0,
由A+B+C=π得A+C=π-B,则sin(A+C)=sinB≠0代入上式得,
sinB-2sinBcosA=0,即cosA=
| 1 |
| 2 |
又0<A<π,则A=
| π |
| 3 |
(2)因为△ABC的面积为2
| 3 |
| 1 |
| 2 |
| 3 |
由余弦定理得,a2=b2+c2-2bccosA=(b+c)2-2bc-2bc×
| 1 |
| 2 |
则12=(b+c)2-3bc=(b+c)2-3×8,
解得b+c=6.
点评:本题考查正弦、余弦定理,三角形的面积公式,两角和的正弦公式和诱导公式,以及整体代换,属于中档题.

练习册系列答案
相关题目
设定点F1(-3,0),F2(3,0),动点P(x,y)满足条件|PF1|+|PF2|=6,则动点P的轨迹是( )
| A、椭圆 | B、线段 |
| C、双曲线 | D、椭圆或线段 |
过点M(1,2)的直线l与圆C:(x-3)2+( y-4)2=25交于A、B两点,C为圆心,当∠ACB最小时,直线l的方程是( )
| A、x-2y+3=0 |
| B、2x+y-4=0 |
| C、x-y+1=0 |
| D、x+y-3=0 |
若sinα=-
,cosα=
,则下列各点在角α终边上的是( )
| 4 |
| 5 |
| 3 |
| 5 |
| A、(-4,3) |
| B、(3,-4) |
| C、(4,-3) |
| D、(-3,4) |
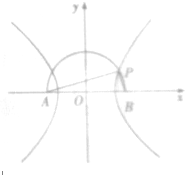 如图,在以点O为圆心,AB为直径的半圆中,P为半圆弧上一点,且AB=4,∠PAB=15°,若A、B分别为双曲线的左、右焦点,则双曲线的标准方程是
如图,在以点O为圆心,AB为直径的半圆中,P为半圆弧上一点,且AB=4,∠PAB=15°,若A、B分别为双曲线的左、右焦点,则双曲线的标准方程是