题目内容
设△ABC的内角A、B、C所对边的长分别为a、b、c,若a,b,c成等差数列,且5sinA=3sinB,则角C为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:正弦定理
专题:解三角形
分析:利用a,b,c成等差数列得到a,b和c的关系式,利用正弦定理和已知等式求得a和b的关系式,分别设出a,b和c,最后利用余弦定理即可求得cosC的值,则C可得.
解答:
解:∵a,b,c成等差数列,
∴2b=a+c,
∵5sinA=3sinB,
∴由正弦定理得5a=3b,
设a=3t,b=5t,则c=7t,
∴cosC=
=
=-
,
∵0<C<π,
∴C=
.
故选C.
∴2b=a+c,
∵5sinA=3sinB,
∴由正弦定理得5a=3b,
设a=3t,b=5t,则c=7t,
∴cosC=
| a2+b2-c2 |
| 2ab |
| 9t2+25t2-49t2 |
| 2×3×5t2 |
| 1 |
| 2 |
∵0<C<π,
∴C=
| 2π |
| 3 |
故选C.
点评:本题主要考查了正弦定理和余弦定理的应用.解题过程中巧妙的运用了正弦定理和余弦定理完成了边和角问题的转化.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
已知集合M={x|x2+2x-3>0},N={x|y=
},则(∁RM)∪N为( )
| ||
| ln(2x-x2) |
| A、[-3,2) |
| B、(-2,3] |
| C、[-3,1)∪(1,2) |
| D、[-1,2) |
(
+
)10的展开式中常数项为( )
| x |
| 1 | |||
|
| A、120 | B、210 |
| C、252 | D、45 |
已知等差数列{an}中,a3+a4=a12,a1+a2=10,则a2+a4+…a100的值等于( )
| A、1300 | ||
| B、1350 | ||
| C、2650 | ||
D、
|
如图所示的程序框图,则输出的结果为( )


| A、189 | B、381 |
| C、93 | D、45 |
已知复数z满足
=i(i为虚数单位),则z的虚部为( )
| 1+z |
| 1-z |
| A、1 | B、-i | C、i | D、-1 |
已知实数x、y满足约束条件
,若向量
=(x,y),向量
=(3,-1).设z表示向量
在向量
方向上的投影,则z的最大值是( )
|
| a |
| b |
| a |
| b |
A、-
| ||||
B、-
| ||||
C、
| ||||
| D、6 |
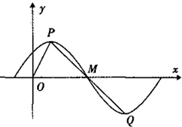 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<