题目内容
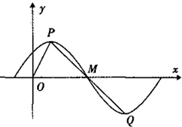 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<| π |
| 2 |
| ||
| 5 |
| 5 |
| 2 |
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)将函数y=f(x)的图象向右平移2个单位后得到函数y=g(x)的图象,试求函数h(x)=f(x)•g(x)图象的对称轴方程.
考点:余弦定理,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的求值
分析:(Ⅰ)设P(x,y),根据cos∠POM的值求出sin∠POM的值,以及|OP|的长,利用任意角的三角函数定义求出x与y的值,确定出P坐标,得到A的值,由三角函数性质得到P,Q关于M对称,求出|PM|的长,设|OM|=m,利用余弦定理列出关系式求出m的值,确定出M坐标,进而求出函数的最小正周期,确定出ω的值,即可确定出函数y=f(x)的解析式;
(Ⅱ)由y=f(x)利用平移规律得到y=g(x)解析式,进而确定出h(x)解析式,利用余弦函数的对称性即可求出h(x)对称轴方程.
(Ⅱ)由y=f(x)利用平移规律得到y=g(x)解析式,进而确定出h(x)解析式,利用余弦函数的对称性即可求出h(x)对称轴方程.
解答:
解:(Ⅰ)设P(x,y),由cos∠POM=
,得到sin∠POM=
,且|OP|=
,
∴
,
解得:
,
∴P(1,2),即A=2,
由三角函数性质得到P,Q关于点M对称,
∴|PM|=2
,
设|OM|=m,由余弦定理得:|OM|2+|OP|2-2|OM||OP|cos∠POM=|PM|2,
即m2-2m-3=0,
解得:m=3或m=-1(舍去),即M=(3,0),
∴函数f(x)的最小正周期T=4×(3-1)=8,即
=8,
∴ω=
,
将P(1,2)代入函数f(x)=2sin(
x+φ),得:sin(
+φ)=1,
∵0<φ<
,∴
<
+φ<
,
∴
+φ=
,即φ=
,
则函数y=f(x)的解析式为2sin(
x+
);
(Ⅱ)∵函数y=f(x)的图象向右平移2个单位后得到函数y=g(x)的图象,
∴y=g(x)=f(x-2)=2sin(
x-
),
∴h(x)=4sin(
x+
)sin(
x-
)=2(sin2
x-cos2
x)=-2cos
x,
令
x=kπ(k∈Z),得到x=2k(k∈Z),
则函数h(x)的对称轴方程是x=2k(k∈Z).
| ||
| 5 |
2
| ||
| 5 |
| 5 |
∴
|
解得:
|
∴P(1,2),即A=2,
由三角函数性质得到P,Q关于点M对称,
∴|PM|=2
| 2 |
设|OM|=m,由余弦定理得:|OM|2+|OP|2-2|OM||OP|cos∠POM=|PM|2,
即m2-2m-3=0,
解得:m=3或m=-1(舍去),即M=(3,0),
∴函数f(x)的最小正周期T=4×(3-1)=8,即
| 2π |
| ω |
∴ω=
| π |
| 4 |
将P(1,2)代入函数f(x)=2sin(
| π |
| 4 |
| π |
| 4 |
∵0<φ<
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
则函数y=f(x)的解析式为2sin(
| π |
| 4 |
| π |
| 4 |
(Ⅱ)∵函数y=f(x)的图象向右平移2个单位后得到函数y=g(x)的图象,
∴y=g(x)=f(x-2)=2sin(
| π |
| 4 |
| π |
| 4 |
∴h(x)=4sin(
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
令
| π |
| 2 |
则函数h(x)的对称轴方程是x=2k(k∈Z).
点评:此题考查了余弦定理,任意角的三角函数定义,三角函数的周期性及其求法,以及平移规律,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
设△ABC的内角A、B、C所对边的长分别为a、b、c,若a,b,c成等差数列,且5sinA=3sinB,则角C为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在四棱锥S-ABCD中,地面ABCD为矩形,侧面SAD为边长2的正三角形,且面SAD⊥面ABCD.AB=
如图,在四棱锥S-ABCD中,地面ABCD为矩形,侧面SAD为边长2的正三角形,且面SAD⊥面ABCD.AB=