题目内容
20.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的渐近线方程为y=±$\frac{{\sqrt{3}}}{3}$x,若顶点到渐近线的距离为$\sqrt{3}$,则双曲线的方程为( )| A. | $\frac{x^2}{4}-\frac{{3{y^2}}}{4}$=1 | B. | $\frac{x^2}{12}-\frac{y^2}{4}$=1 | C. | $\frac{x^2}{4}-\frac{y^2}{12}$=1 | D. | $\frac{{3{x^2}}}{4}-\frac{y^2}{4}$=1 |
分析 根据题意,结合双曲线的方程由点到直线的距离公式可得顶点到渐近线的距离为$\frac{a}{2}=\sqrt{3}$,解可得a的值,即可得b的值,代入双曲线的方程即可得答案.
解答 解:根据题意,双曲线渐近线方程为y=±$\frac{{\sqrt{3}}}{3}$x,变形可得$x±\sqrt{3}y=0$,
顶点坐标(a,0),顶点到渐近线的距离为$\frac{a}{2}=\sqrt{3}$,
解得$a=2\sqrt{3}$,
根据渐近线方程的斜率$\frac{b}{a}=\frac{{\sqrt{3}}}{3}$,可得b=2,
所以双曲线的方程为$\frac{x^2}{12}-\frac{y^2}{4}=1$;
故选:B.
点评 本题考查双曲线的几何性质,关键是掌握双曲线的标准方程与渐近线方程的关系.

练习册系列答案
相关题目
8.已知函数$f(x)=kx(x∈[\frac{1}{e},e])$,$g(x)={(\frac{1}{e})^{\frac{x}{2}}}$,若f(x),g(x)图象上分别存在点M,N,使得M,N关于直线y=x对称,则实数k的取值范围为( )
| A. | $[-\frac{1}{e},e]$ | B. | $[-\frac{2}{e},2e]$ | C. | $[-\frac{3}{e},3e]$ | D. | $(-\frac{2}{e},2e)$ |
10.已知i为虚数单位,复数z满足z(1-i)=1+i,则z2017=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
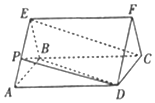 如图,三棱柱ABE-DCF中,△EAB是正三角形,四边形ABCD是矩形,且EA=2,BC=2$\sqrt{3}$,EC=4.
如图,三棱柱ABE-DCF中,△EAB是正三角形,四边形ABCD是矩形,且EA=2,BC=2$\sqrt{3}$,EC=4.