题目内容
9.已知等比数列{an}中,a1=3,a4=24,(1)求数列{an}的通项公式;
(2)设等差数列{bn}中,b2=a2,b9=a5,求数列{bn}的前n项和Sn.
分析 (1)利用等比数列的通项公式即可得出.
(2)利用等差数列的通项公式与求和公式即可得出.
解答 解:(1)设等比数列的公比为q,由已知,得24=3q3,解得q=2,
∴${a_n}={a_1}•{q^{n-1}}=3•{2^{n-1}}$.
(2)由(1)得a2=6,a5=48,
∴b2=6,b9=48.
设等差数列{bn}的公差为d,则$\left\{\begin{array}{l}{b_1}+d=6\\{b_1}+8d=48\end{array}\right.$
解得$\left\{\begin{array}{l}{b_1}=0\\ d=6\end{array}\right.$,
∴${S_n}=n{b_1}+\frac{n(n-1)}{2}d=3{n^2}-3n$.
点评 本题考查了等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的渐近线方程为y=±$\frac{{\sqrt{3}}}{3}$x,若顶点到渐近线的距离为$\sqrt{3}$,则双曲线的方程为( )
| A. | $\frac{x^2}{4}-\frac{{3{y^2}}}{4}$=1 | B. | $\frac{x^2}{12}-\frac{y^2}{4}$=1 | C. | $\frac{x^2}{4}-\frac{y^2}{12}$=1 | D. | $\frac{{3{x^2}}}{4}-\frac{y^2}{4}$=1 |
14.已知复数z=$\frac{1+2i}{2}$(1+i)2(i为虚数单位),则z的共轭复数是( )
| A. | -2-i | B. | 2+3i | C. | $\frac{1}{2}$-i | D. | $\frac{1}{2}+i$ |
1.已知i是虚数单位,复数z满足z(3+4i)=1+i,则复平面内表示z的共轭复数的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.在区间[0,1]上随机选取两个数x和y,则y>2x的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
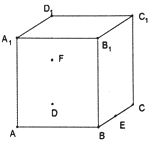 在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,
在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,