题目内容
10．已知i为虚数单位，复数z满足z（1-i）=1+i，则z2017=（ ）| A． | 1 | B． | -1 | C． | i | D． | -i |
分析 化简z，直接利用虚数单位i的运算性质化简得答案．
解答 解：∵z（1-i）=1+i，
∴z=$\frac{1+i}{1-i}$=$\frac{（1+i）（1+i）}{（1-i）（1+i）}$=i，
则z2017=i2017=i504×4+1=i，
故选：C．
点评 本题考查复数代数形式的乘除运算，考查了虚数单位i的性质，是基础题．
练习册系列答案
相关题目
20．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的渐近线方程为y=±$\frac{{\sqrt{3}}}{3}$x，若顶点到渐近线的距离为$\sqrt{3}$，则双曲线的方程为（ ）
| A． | $\frac{x^2}{4}-\frac{{3{y^2}}}{4}$=1 | B． | $\frac{x^2}{12}-\frac{y^2}{4}$=1 | C． | $\frac{x^2}{4}-\frac{y^2}{12}$=1 | D． | $\frac{{3{x^2}}}{4}-\frac{y^2}{4}$=1 |
1．已知i是虚数单位，复数z满足z（3+4i）=1+i，则复平面内表示z的共轭复数的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
18．在区间[0，1]上随机选取两个数x和y，则y＞2x的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{1}{3}$ |
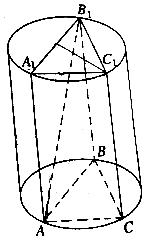如图，圆柱有一个高6$\sqrt{2}$cm，体积为54$\sqrt{6}$cm3的内接正三棱柱ABC-A1B1C1．