题目内容
15.若曲线f(x)=x3-ax2+b在点(1,f(1))处切线的倾斜角为$\frac{3π}{4}$,则a等于( )| A. | 2 | B. | -2 | C. | 3 | D. | -1 |
分析 求得导函数,利用f(x)=x3-ax2+b在点(1,f(1))处切线的倾斜角为$\frac{3π}{4}$,可得f′(1)=-1,由此可求a的值.
解答 解:求导函数可得f′(x)=3x2-2ax
∵函数f(x)=x3-ax2+b在x=1处的切线倾斜角为$\frac{3π}{4}$,
∴f′(1)=-1,
∴3-2a=-1,
∴a=2.
故选:A.
点评 本题考查导数的几何意义,考查学生的计算能力,属于基础题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
5.将函数y=$\sqrt{3}cosx+sinx({x∈R})$的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
20.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的渐近线方程为y=±$\frac{{\sqrt{3}}}{3}$x,若顶点到渐近线的距离为$\sqrt{3}$,则双曲线的方程为( )
| A. | $\frac{x^2}{4}-\frac{{3{y^2}}}{4}$=1 | B. | $\frac{x^2}{12}-\frac{y^2}{4}$=1 | C. | $\frac{x^2}{4}-\frac{y^2}{12}$=1 | D. | $\frac{{3{x^2}}}{4}-\frac{y^2}{4}$=1 |
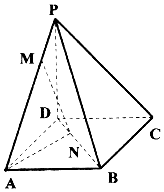 如图,四棱锥P-ABCD底面为正方形,已知PD⊥平面ABCD,PD=AD,点M为线段PA上任意一点(不含端点),点N在线段BD上,且PM=DN.
如图,四棱锥P-ABCD底面为正方形,已知PD⊥平面ABCD,PD=AD,点M为线段PA上任意一点(不含端点),点N在线段BD上,且PM=DN.