题目内容
10.三棱锥A-BCD中,AB,AC,AD两两垂直,其外接球半径为2,设三棱锥A-BCD的侧面积为S,则S的最大值为8.分析 三棱锥A-BCD的三条侧棱两两互相垂直,所以把它扩展为长方体,它也外接于球,对角线的长为球的直径,然后利用基本不等式解答即可.
解答 解:设AB,AC,AD分别为a,b,c,则三棱锥A-BCD的三条侧棱两两互相垂直,所以把它扩展为长方体,
它也外接于球,对角线的长为球的直径,∴a2+b2+c2=16,
S=$\frac{1}{2}$(ab+bc+ac)≤$\frac{1}{2}$(a2+b2+c2)=8,
故答案为:8.
点评 本题考查三棱锥A-BCD的侧面积,考查学生空间想象能力,解答的关键是构造球的内接长方体,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知棱长为$\sqrt{3}$的正方体ABCD-A1B1C1D1内部有一圆柱,此圆柱恰好以直线AC1为轴,则该圆柱侧面积的最大值为( )
| A. | $\frac{{9\sqrt{2}}}{8}π$ | B. | $\frac{{9\sqrt{2}}}{4}π$ | C. | $2\sqrt{3}π$ | D. | $3\sqrt{2}π$ |
1.曲线y=-ln(2x+1)+2在点(0,2)处的切线与直线y=0和y=2x围成的三角形的面积为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
5.将函数y=$\sqrt{3}cosx+sinx({x∈R})$的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
15.在下列函数中,最小值为2的是( )
| A. | y=2x+2-x | B. | y=sinx+$\frac{1}{sinx}$(0<x<$\frac{π}{2}$) | ||
| C. | y=x+$\frac{1}{x}$ | D. | y=log3x+$\frac{1}{lo{g}_{3}x}$(1<x<3) |
2.$\frac{1-tan17°tan28°}{tan17°+tan28°}$等于( )
| A. | -1 | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
20.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的渐近线方程为y=±$\frac{{\sqrt{3}}}{3}$x,若顶点到渐近线的距离为$\sqrt{3}$,则双曲线的方程为( )
| A. | $\frac{x^2}{4}-\frac{{3{y^2}}}{4}$=1 | B. | $\frac{x^2}{12}-\frac{y^2}{4}$=1 | C. | $\frac{x^2}{4}-\frac{y^2}{12}$=1 | D. | $\frac{{3{x^2}}}{4}-\frac{y^2}{4}$=1 |
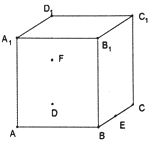 在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,
在棱长为2的正方体ABCD-A1B1C1D1中,E是BC的中点,F是DD1的中点,