题目内容
8.某高中组织数学知识竞赛,采取答题闯关的形式,分两种题型,每种题型设两关.“数学文化”题答对一道得5分,“数学应用”题答对一道得10分,答对一道题即可进入下一关,否则终止比赛.有甲、乙、丙三人前来参赛,设三人答对每道题的概率分别是$\frac{3}{4}$、$\frac{2}{3}$、$\frac{1}{2}$,三人答题互不影响.甲、乙选择“数学文化”题,丙选择“数学应用”题.(Ⅰ)求乙、丙两人所得分数相等的概率;
(Ⅱ)设甲、丙两人所得分数之和为随机变量X,求X的分布列与期望.
分析 (Ⅰ)乙、丙所得分数相等时,应为0分或10分,计算对应的概率值即可;
(Ⅱ)根据题意,X的可能取值为0,5,10,15,20,25,30,求出对应的概率值,写出X的分布列,再计算数学期望值.
解答 解:(Ⅰ)乙、丙所得分数相等时,应为0分或10分,
其概率为P=(1-$\frac{2}{3}$)×(1-$\frac{1}{2}$)+$\frac{2}{3}$×$\frac{2}{3}$×$\frac{1}{2}$×(1-$\frac{1}{2}$)=$\frac{5}{18}$;
(Ⅱ)设甲、丙两人所得分数之和为随机变量X,则X的可能取值为0,5,10,15,20,25,30,
其概率为P(X=0)=(1-$\frac{2}{3}$)×(1-$\frac{1}{2}$)=$\frac{1}{6}$,
P(X=5)=$\frac{2}{3}$×(1-$\frac{2}{3}$)×(1-$\frac{1}{2}$)=$\frac{1}{9}$,
P(X=10)=$\frac{2}{3}$×$\frac{2}{3}$×(1-$\frac{1}{2}$)+(1-$\frac{2}{3}$)×$\frac{1}{2}$×(1-$\frac{1}{2}$)=$\frac{11}{36}$,
P(X=15)=$\frac{2}{3}$×$\frac{1}{2}$×(1-$\frac{2}{3}$)×(1-$\frac{1}{2}$)=$\frac{1}{18}$,
P(X=20)=$\frac{2}{3}$×$\frac{2}{3}$×$\frac{1}{2}$×(1-$\frac{1}{2}$)+(1-$\frac{2}{3}$)×$\frac{1}{2}$×$\frac{1}{2}$=$\frac{7}{36}$,
P(X=25)=$\frac{2}{3}$×(1-$\frac{2}{3}$)×$\frac{1}{2}×\frac{1}{2}$=$\frac{1}{18}$,
P(X=30)=$\frac{2}{3}$×$\frac{2}{3}$×$\frac{1}{2}×\frac{1}{2}$=$\frac{1}{9}$;
∴X的分布列为:
| X | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| P | $\frac{1}{6}$ | $\frac{1}{9}$ | $\frac{11}{36}$ | $\frac{1}{18}$ | $\frac{7}{36}$ | $\frac{1}{18}$ | $\frac{1}{9}$ |
点评 本题考查了离散型随机变量的分布列与数学期望的计算问题,也考查了分析与计算能力,是综合题.

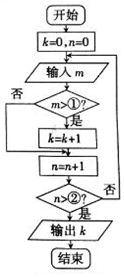 现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是( )
现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是( )| A. | 14,19 | B. | 14,20 | C. | 15,19 | D. | 15,20 |
| A. | -3<k<1 | B. | k>1 | C. | -1<k<1 | D. | -1<k<3 |
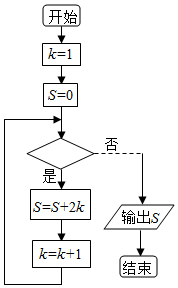 如果执行如图的程序框图,输出的S=30,则判断框处为( )
如果执行如图的程序框图,输出的S=30,则判断框处为( )| A. | k<5 | B. | k≤5 | C. | k≥6 | D. | k>6 |
| A. | -4 | B. | -1 | C. | 2 | D. | 5 |
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |