题目内容
11.不等式|x+3|-|x-1|≤2a对任意实数x恒成立,则实数a的取值范围是( )| A. | (-∞,-2] | B. | (-∞,-2]∪[2,+∞) | C. | [2,+∞) | D. | a∈R |
分析 令f(x)=|x+3|-|x-1|,写出分段函数,求得f(x)的最大值4,由2a≥4求得实数a的取值范围.
解答 解:令f(x)=|x+3|-|x-1|=$\left\{\begin{array}{l}{-4,x<-3}\\{2x+2,-3≤x≤1}\\{4,x>1}\end{array}\right.$,
作出图象如图,
∴f(x)≤4,
∵不等式|x+3|-|x-1|≤2a对任意实数x恒成立,
∴2a≥4,得a≥2.
∴实数a的取值范围是[2,+∞).
故选:C.
点评 本题考查含有绝对值的不等式的解法,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
20.若长方体的一个顶点上三条棱长分别是1、1、2,且它的八个顶点都在同一球面上,则这个球的表面积是( )
| A. | 6π | B. | 4π | C. | 3π | D. | 12π |
1.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左顶点为A(-1,0),右焦点为F2($\sqrt{3}$,0),则双曲线的渐近线方程为( )
| A. | y=±$\sqrt{2}$x | B. | y=±2x | C. | y=±$\frac{\sqrt{2}}{2}$x | D. | y=±$\frac{1}{2}$x |
16.已知函数f(x)=ax3+2x2-1有且只有两个零点,则实数a的取值集合( )
| A. | {-1,0,1} | B. | {0,$\frac{4\sqrt{6}}{9}$} | C. | {0,$\frac{2\sqrt{3}}{3}$} | D. | {-$\frac{4\sqrt{6}}{9}$,0,$\frac{4\sqrt{6}}{9}$} |
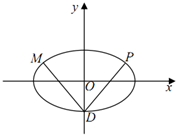 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到直线x=$\frac{a}{e}$的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到直线x=$\frac{a}{e}$的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.