题目内容
16.已知函数f(x)=ax3+2x2-1有且只有两个零点,则实数a的取值集合( )| A. | {-1,0,1} | B. | {0,$\frac{4\sqrt{6}}{9}$} | C. | {0,$\frac{2\sqrt{3}}{3}$} | D. | {-$\frac{4\sqrt{6}}{9}$,0,$\frac{4\sqrt{6}}{9}$} |
分析 当a=0时,函数f(x)=2x2-1有且只有两个零点,满足条件;当a≠0时,函数的极值为0,进而得到答案.
解答 解:当a=0时,函数f(x)=2x2-1有且只有两个零点,满足条件;
当a≠0时,令f′(x)=3ax2+4x=0,解得:x=0,或x=-$\frac{4}{3a}$,
∵f(0)=1≠0,
∴f(-$\frac{4}{3a}$)=$\frac{32}{27{a}^{2}}-1=0$,
解得:a=$±\frac{4\sqrt{6}}{9}$,
故a∈{-$\frac{4\sqrt{6}}{9}$,0,$\frac{4\sqrt{6}}{9}$},
故选:D
点评 本题考查的知识点是函数的零点及零点个数,分类讨论思想,难度中档.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
6.在复平面内,复数z=-2+i对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.不等式|x+3|-|x-1|≤2a对任意实数x恒成立,则实数a的取值范围是( )
| A. | (-∞,-2] | B. | (-∞,-2]∪[2,+∞) | C. | [2,+∞) | D. | a∈R |
1.已知函数f(x)=$\left\{\begin{array}{l}{x^2}+1,x≤0\\-x+1,x>0\end{array}$,若a=f(${log_2}\frac{1}{3}$),b=f(${2^{\frac{1}{3}}}$),c=f(${3^{-\frac{1}{2}}}$),则( )
| A. | a>b>c | B. | c>b>a | C. | a>c>b | D. | b>c>a |
6.已知集合A={x|x2-x-2<0},B=$\{x|y=lg\frac{1-x}{1+x}\}$,在区间(-3,3)上任取一实数x,则x∈A∩B的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{12}$ |
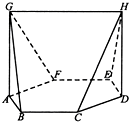 如图,在七面体ABCDEFGH中,底面ABCDEF是边长为2的正六边形,AG=DH=3,且
如图,在七面体ABCDEFGH中,底面ABCDEF是边长为2的正六边形,AG=DH=3,且