题目内容
3.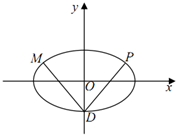 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到直线x=$\frac{a}{e}$的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到直线x=$\frac{a}{e}$的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.(1)求椭圆C的标准方程;
(2)若过D点作两条相互垂直的直线分别与椭圆C相交于点P,M.求证:直线PM经过一定点.
分析 (1)由题意可得:e=$\frac{c}{a}$=$\frac{2\sqrt{2}}{3}$,$\frac{a}{e}$-c=$\frac{\sqrt{2}}{4}$,a2=b2+c2.联立解出即可得出.
(2)设DP的方程为:y=kx-1,(k≠0),则DM的方程为:y=-$\frac{1}{k}$x-1.分别与椭圆方程联立可得点P,M,利用点斜式可得直线PM的方程,令x=0,解得y,即可得出直线PM经过一定点.
解答 解:(1)由题意可得:e=$\frac{c}{a}$=$\frac{2\sqrt{2}}{3}$,$\frac{a}{e}$-c=$\frac{\sqrt{2}}{4}$,
a2=b2+c2.
联立解得:a=3,c=2$\sqrt{2}$,b=1.
∴椭圆C的标准方程是$\frac{{x}^{2}}{9}$+y2=1.
证明:(2)D(0,-1),设DP的方程为:y=kx-1,(k≠0),
则DM的方程为:y=-$\frac{1}{k}$x-1.
联立$\left\{\begin{array}{l}{y=kx-1}\\{{x}^{2}+9{y}^{2}=9}\end{array}\right.$,化为(1+9k2)x2-18kx=0,
解得x=0或$\frac{18k}{1+9{k}^{2}}$.
则xP=$\frac{18k}{1+9{k}^{2}}$,可得yP=kxP-1=$\frac{9{k}^{2}-1}{1+9{k}^{2}}$.
∴P$(\frac{18k}{1+9{k}^{2}},\frac{9{k}^{2}-1}{1+9{k}^{2}})$.
同理可得:M$(\frac{-18k}{{k}^{2}+9},\frac{9-{k}^{2}}{{k}^{2}+9})$,
kPM=$\frac{\frac{9{k}^{2}-1}{1+9{k}^{2}}-\frac{9-{k}^{2}}{{k}^{2}+9}}{\frac{18k}{1+9{k}^{2}}-\frac{-18k}{{k}^{2}+9}}$=.$\frac{{k}^{2}-1}{10k}$
∴直线PM的方程为:y-$\frac{9{k}^{2}-1}{1+9{k}^{2}}$=$\frac{{k}^{2}-1}{10k}$$(x-\frac{18k}{1+9{k}^{2}})$,
令x=0,则y=$\frac{9{k}^{2}-1}{1+9{k}^{2}}$-$\frac{{k}^{2}-1}{10k}$×$\frac{18k}{1+9{k}^{2}}$=$\frac{4}{5}$.
∴直线PM经过一定点$(0,\frac{4}{5})$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、相互垂直的直线斜率之间的关系、直线经过定点问题,考查了推理能力与计算能力,属于难题.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案| A. | $\frac{1}{2}$ | B. | $\frac{1}{16}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
| A. | 4x±9y=0 | B. | 9x±4y=0 | C. | 3x±2y=0 | D. | 2x±3y=0 |
| A. | (-∞,-2] | B. | (-∞,-2]∪[2,+∞) | C. | [2,+∞) | D. | a∈R |
| A. | 1-i | B. | 1+i | C. | 2-2i | D. | 2+2i |
| A. | 0.40 | B. | 0.41 | C. | 0.43 | D. | 0.44 |