题目内容
已知函数f(x)=x2-px+3.
(1)若f(0)=f(4),求不等式f(x)≤0的解集;
(2)若函数f(x)在[1,+∞)上是增函数,求p的取值范围;
(3)当p=2时,若函数在[0,m]上的最大值为3,最小值为2,求m的取值范围.
(1)若f(0)=f(4),求不等式f(x)≤0的解集;
(2)若函数f(x)在[1,+∞)上是增函数,求p的取值范围;
(3)当p=2时,若函数在[0,m]上的最大值为3,最小值为2,求m的取值范围.
考点:二次函数在闭区间上的最值,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)先求出对称轴,得到p的值,再解不等式即可.
(2)函数为开口向上,故对称轴小于等于1,解得即可,
(3)利用对称轴,求出函数的最值即可.
(2)函数为开口向上,故对称轴小于等于1,解得即可,
(3)利用对称轴,求出函数的最值即可.
解答:
解:(1)∵f(0)=f(4),
∴f(x)的对称轴为x=2,
∴p=4,
所以不等式f(x)≤0,
即为x2-4x+3≤0,
所以其解集为{x|1≤x≤3}.
(2)∵函数f(x)在[1,+∞)上是增函数,
所以函数f(x)的对称轴x=
在直线x=1的左侧或与x=1重合,
即
≤1,
∴p≤2.
(3)当p=2时,f(x)=x2-2x+3.其对称轴为x=1,
f(x)min=f(1)=2.
又f(0)=3,f(2)=3,
∴1≤m≤2.
∴f(x)的对称轴为x=2,
∴p=4,
所以不等式f(x)≤0,
即为x2-4x+3≤0,
所以其解集为{x|1≤x≤3}.
(2)∵函数f(x)在[1,+∞)上是增函数,
所以函数f(x)的对称轴x=
| p |
| 2 |
即
| p |
| 2 |
∴p≤2.
(3)当p=2时,f(x)=x2-2x+3.其对称轴为x=1,
f(x)min=f(1)=2.
又f(0)=3,f(2)=3,
∴1≤m≤2.
点评:本题主要考查了二次函数的图象和性质,属于基础题.

练习册系列答案
相关题目
方程lnx=6-2x的根必定属于区间( )
| A、(-2,1) | ||||
B、(
| ||||
C、(1,
| ||||
D、(
|
把正整数按如图所示的规律排列,则从2003到2005的箭头方向依次为( )


| A、↓ 2004→ |
| B、↑ →2004 |
| C、2004→ ↑ |
| D、→2004 ↓ |
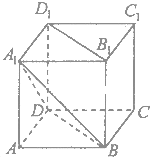 如图,在正方体ABCD-A1B1C1D1中,AB=2.
如图,在正方体ABCD-A1B1C1D1中,AB=2.