题目内容
(x-2)(x-1)5的展开式中x2项的系数为 .(用数字作答)
考点:二项式定理的应用
专题:二项式定理
分析:把(x-1)5 按照二项式定理展开,可得(x-2)(x-1)5的展开式中x2项的系数.
解答:
解:∵(x-2)•(x-1)5 =(x-2)•(x5-
•x4+
•x3-
•x2+
•x-
),
故展开式中x2项的系数为
+2
=25,
故答案为:25.
| C | 1 5 |
| C | 2 5 |
| C | 3 5 |
| C | 4 5 |
| C | 5 5 |
故展开式中x2项的系数为
| C | 4 5 |
| C | 3 5 |
故答案为:25.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.

练习册系列答案
相关题目
点(x,y)的坐标x,y都是有理数时,该点称为有理点,在半径为r,圆心为(a,b)的圆中,若a∈Q,b∈Q,则这个圆上的有理点的数目为( )
| A、最多有一个 |
| B、最多有两个 |
| C、最多有三个 |
| D、可以有无穷多个 |
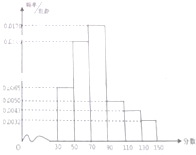 某县为“中学生知识竞赛”进行选取性测试,规定:成绩大于或等于90分的右参赛资格,90分以下(不包括90分)的则被淘汰,若现有1000人参加测试,学生成绩的频率分别直方图如图:
某县为“中学生知识竞赛”进行选取性测试,规定:成绩大于或等于90分的右参赛资格,90分以下(不包括90分)的则被淘汰,若现有1000人参加测试,学生成绩的频率分别直方图如图: