题目内容
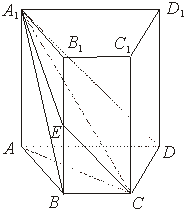 如图,四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,且A1A=4.梯形ABCD的面积为6,且AD∥BC,AD=2BC,AB=2.平面A1DCE与B1B交于点E.
如图,四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,且A1A=4.梯形ABCD的面积为6,且AD∥BC,AD=2BC,AB=2.平面A1DCE与B1B交于点E.(1)证明:EC∥A1D;
(2)求点C到平面ABB1A1的距离.
考点:点、线、面间的距离计算,直线与平面平行的性质
专题:空间位置关系与距离
分析:(1)通过证明BE∥平面AA1D.BC∥平面AA1D,然后证明平面BCE∥平面ADA1,利用平面与平面平行的性质定理证明:EC∥A1D;
(2)法一:直接利用等体积方法,VC-A1AB=VA1-ABC,即可求点C到平面ABB1A1的距离.
法二:证明CF⊥面A1ABB1,即线段CF的长为点C到平面ABB1A1的距离.利用S△ABC=
S△ACD=
S梯形ABCD=2又S△ABC=
AB•CF,求出CF=2,即点C到平面ABB1A1的距离为2.
(2)法一:直接利用等体积方法,VC-A1AB=VA1-ABC,即可求点C到平面ABB1A1的距离.
法二:证明CF⊥面A1ABB1,即线段CF的长为点C到平面ABB1A1的距离.利用S△ABC=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
解答:

 (本小题满分14分)
(本小题满分14分)
(1)证明:因为BE∥AA1,AA1?平面AA1D,BE?平面AA1D,所以BE∥平面AA1D.(1分)
因为BC∥AD,AD?平面AA1D,BC?平面AA1D,所以BC∥平面AA1D.(2分)
又BE∩BC=B,BE?平面BCE,BC?平面BCE,所以平面BCE∥平面ADA1.(4分)
又平面A1DCE∩平面BCE=EC,平面A1DCE∩平面A1AD=A1D,
所以EC∥A1D.(6分)
(2)解法一:因为S梯形ABCD=6,BC∥AD,AD=2BC,
所以S△ABC=
S△ACD=
S梯形ABCD=2.(9分)
因为A1A⊥底面ABCD,AB?底面ABCD,所以A1A⊥AB.
所以S△A1AB=
A1A•AB=4.(10分)
设点C到平面ABB1A1的距离为h,因为VC-A1AB=VA1-ABC,(12分)
所以
h•S△A1AB=
A1A•S△ABC,(13分)
所以h=2,即点C到平面ABB1A1的距离为2.(14分)
解法二:如图,在平面ABC中,作CF⊥AB于F.(7分)
因为A1A⊥底面ABCD,CF?底面ABCD,
所以CF⊥A1A.(8分)
又A1A∩AB=A,所以CF⊥面A1ABB1.(9分)
即线段CF的长为点C到平面ABB1A1的距离.
因为S梯形ABCD=6,BC∥AD,AD=2BC,
所以S△ABC=
S△ACD=
S梯形ABCD=2(12分)
又S△ABC=
AB•CF,(13分)
所以CF=2,即点C到平面ABB1A1的距离为2.(14分)

 (本小题满分14分)
(本小题满分14分)(1)证明:因为BE∥AA1,AA1?平面AA1D,BE?平面AA1D,所以BE∥平面AA1D.(1分)
因为BC∥AD,AD?平面AA1D,BC?平面AA1D,所以BC∥平面AA1D.(2分)
又BE∩BC=B,BE?平面BCE,BC?平面BCE,所以平面BCE∥平面ADA1.(4分)
又平面A1DCE∩平面BCE=EC,平面A1DCE∩平面A1AD=A1D,
所以EC∥A1D.(6分)
(2)解法一:因为S梯形ABCD=6,BC∥AD,AD=2BC,
所以S△ABC=
| 1 |
| 2 |
| 1 |
| 3 |
因为A1A⊥底面ABCD,AB?底面ABCD,所以A1A⊥AB.
所以S△A1AB=
| 1 |
| 2 |
设点C到平面ABB1A1的距离为h,因为VC-A1AB=VA1-ABC,(12分)
所以
| 1 |
| 3 |
| 1 |
| 3 |
所以h=2,即点C到平面ABB1A1的距离为2.(14分)
解法二:如图,在平面ABC中,作CF⊥AB于F.(7分)
因为A1A⊥底面ABCD,CF?底面ABCD,
所以CF⊥A1A.(8分)
又A1A∩AB=A,所以CF⊥面A1ABB1.(9分)
即线段CF的长为点C到平面ABB1A1的距离.
因为S梯形ABCD=6,BC∥AD,AD=2BC,
所以S△ABC=
| 1 |
| 2 |
| 1 |
| 3 |
又S△ABC=
| 1 |
| 2 |
所以CF=2,即点C到平面ABB1A1的距离为2.(14分)
点评:本题考查平面与平面平行的性质定理的应用,点到平面的距离的求法,考查计算能力以及空间想象能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若关于x的方程4x+m•2x+1+m2-m-2=0有解,则实数m的取值范围是( )
| A、[-2,-1) |
| B、[-2,0) |
| C、[-2,2) |
| D、[-2,+∞) |
已知底面边长为
,侧棱长为6的正四棱柱的各顶点均在同一个球面上,其对角线为直径,则该球的体积为( )
| 3 |
A、
| ||
B、7
| ||
C、
| ||
D、
|