题目内容
一颗正方体骰子，其六个面上的点数分别为1，2，3，4，5，6，现将这颗骰子抛掷三次，观察向上的点数，则三次点数之和等于15的概率为 ．
考点：古典概型及其概率计算公式
专题：计算题,概率与统计
分析：这颗骰子连续抛掷三次，三次向上的点数一共有63种情况，满足条件的事件是三次点数之和是15，可以列举出所有的事件，共有10种结果，得到概率．
解答：
解：将这颗骰子连续抛掷三次，三次向上的点数一共有63种情况，
满足条件的事件是三次点数之和是15，
可以列举出所有的事件663，636，366，456，465，645，654，546，564，555共有10种结果，
∴三次点数之和是15的概率是
=
．
故答案为：
．
满足条件的事件是三次点数之和是15，
可以列举出所有的事件663，636，366，456，465，645，654，546，564，555共有10种结果，
∴三次点数之和是15的概率是
| 10 |
| 216 |
| 5 |
| 108 |
故答案为：
| 5 |
| 108 |
点评：本题考查概率的性质和应用，解题时要认真审题，研究对象是由有限个元素构成的集合时，把所有对象一一列举出来，再对其一一进行研究，注意列举法的合理运用．
练习册系列答案
相关题目
已知函数f（x）的导函数为f′（x），且满足f′（x）＜2f（x），则（ ）
| A、f（2）＞e2f（1） |
| B、e2f（0）＞f（1） |
| C、9f（ln2）＜4f（ln3） |
| D、e2f（ln2）＜4f（1） |
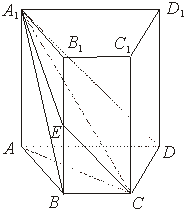如图，四棱柱ABCD-A1B1C1D1中，A1A⊥底面ABCD，且A1A=4．梯形ABCD的面积为6，且AD∥BC，AD=2BC，AB=2．平面A1DCE与B1B交于点E．