题目内容
设P:指数函数y=ax在x∈R内单调递减;Q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果P为真,Q为假,求a的取值范围.
考点:复合命题的真假
专题:阅读型
分析:利用指数函数的单调性及曲线相交的条件,分别求出命题命题P为真和命题Q为假时a的取值范围,再求交集.
解答:
解:∵当0<a<1时,指数函数y=ax在R内单调递减;
∴命题P为真,则0<a<1;
曲线y=x2+(2a-3)x+1与x轴有两个不同的交点?△=(2a-3)2-4>0,
即a<
或a>
.
∴命题Q为假,则
≤a≤
,
∴P为真,Q为假,a的取值范围为[
,1).
∴命题P为真,则0<a<1;
曲线y=x2+(2a-3)x+1与x轴有两个不同的交点?△=(2a-3)2-4>0,
即a<
| 1 |
| 2 |
| 5 |
| 2 |
∴命题Q为假,则
| 1 |
| 2 |
| 5 |
| 2 |
∴P为真,Q为假,a的取值范围为[
| 1 |
| 2 |
点评:本题借助考查复合命题的真假判定,考查了指数函数的单调性及曲线的交点问题,熟练掌握指数函数的单调性及曲线相交的条件是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 已知椭圆
已知椭圆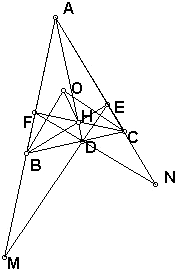 如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OB⊥DF.
如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OB⊥DF.