题目内容
设△ABC的三个内角A,B,C,向量
=(2cosA,sinA),
=(cosB,-2sinB),且
•
=1
(1)求角C的大小:
(2)若△ABC的三边长构成公差为4的等差数列,求△ABC的面积.
| m |
| n |
| m |
| n |
(1)求角C的大小:
(2)若△ABC的三边长构成公差为4的等差数列,求△ABC的面积.
考点:余弦定理,平面向量数量积的运算,正弦定理
专题:解三角形
分析:(1)通过向量的数量积以及两角和与差的三角函数结合三角形的内角和,求出角C的大小:
(2)三角形三边构成公差为4的等差数列,设中间的一条边为x,则最大的边为x+4,最小的边为x-4,根据余弦定理表示出cos120°的式子,将各自设出的值代入即可得到关于x的方程,求出方程的解即可得到三角形的边长,然后利用三角形的面积公式即可求出三角形ABC的面积.
(2)三角形三边构成公差为4的等差数列,设中间的一条边为x,则最大的边为x+4,最小的边为x-4,根据余弦定理表示出cos120°的式子,将各自设出的值代入即可得到关于x的方程,求出方程的解即可得到三角形的边长,然后利用三角形的面积公式即可求出三角形ABC的面积.
解答:
解:(1)△ABC的三个内角A,B,C,向量
=(2cosA,sinA),
=(cosB,-2sinB),且
•
=1
∴2cosAcosB-2sinBsinA=1,
∴cos(A+B)=
.
即cosC=-
,
∴角C=
:
(2)设三角形的三边分别为x-4,x,x+4,
则cos120°=
=-
,
化简得:x-16=4-x,解得x=10,
所以三角形的三边分别为:6,10,14
则△ABC的面积S=
×6×10sin120°=15
.
| m |
| n |
| m |
| n |
∴2cosAcosB-2sinBsinA=1,
∴cos(A+B)=
| 1 |
| 2 |
即cosC=-
| 1 |
| 2 |
∴角C=
| 2π |
| 3 |
(2)设三角形的三边分别为x-4,x,x+4,
则cos120°=
| x2+(x-4)2-(x+4)2 |
| 2x(x-4) |
| 1 |
| 2 |
化简得:x-16=4-x,解得x=10,
所以三角形的三边分别为:6,10,14
则△ABC的面积S=
| 1 |
| 2 |
| 3 |
点评:此题考查学生掌握等差数列的性质,灵活运用余弦定理及三角形的面积公式化简求值,向量的数量积以及两角和与差的三角函数,是一道中档题.

练习册系列答案
相关题目
如果a>b,那么下列不等式中正确的是( )
| A、algx>blgx(x>0) |
| B、ax2>bx2 |
| C、a2>b2 |
| D、2x•a>2x•b |
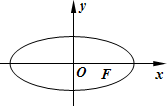 已知椭圆
已知椭圆