题目内容
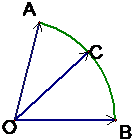给定两个长度为1的平面向量| OA |
| OB |
| 2π |
| 3 |
 |
| AB |
| OC |
| OA |
| OB |
考点：平面向量的基本定理及其意义
专题：计算题,平面向量及应用
分析：对
=x
+y
，两边平方并根据已知条件可得到：x2-xy+y2=（x+y）2-3xy=1，所以（x+y）2-1=3xy，因为根据向量加法的平行四边形法则可知，x，y＞0，所以xy≤
，所以（x+y）2-1≤
（x+y）2，所以得到x+y≤2，所以x+y的最大值是2．
| OC |
| OA |
| OB |
| (x+y)2 |
| 4 |
| 3 |
| 4 |
解答：
解：由已知条件知：
2=1=（x
+y
）2=x2-xy+y2=（x+y）2-3xy；
∴（x+y）2-1=3xy，根据向量加法的平行四边形法则，容易判断出x，y＞0，
∴x+y≥2
，∴xy≤
；
∴（x+y）2-1≤
（x+y）2，∴（x+y）2≤4，∴x+y≤2，即x+y的最大值为2．
| OC |
| OA |
| OB |
∴（x+y）2-1=3xy，根据向量加法的平行四边形法则，容易判断出x，y＞0，
∴x+y≥2
| xy |
| (x+y)2 |
| 4 |
∴（x+y）2-1≤
| 3 |
| 4 |
点评：考查向量数量积的运算及计算公式，向量加法的平行四边形法则，基本不等式．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
若将函数y=2sin（x+
）的图象上各点的横坐标缩短为原来的
倍（纵坐标不变），再向右平移
个单位，则所得图象的一条对称轴的方程为（ ）
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
D、x=
|
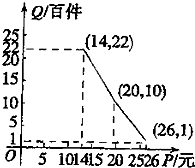在对口扶贫活动中，企业甲将经营状况良好的某种消费品专卖店以优惠价格转让给小型残疾人企业乙，并约定从该店经营的利润中，首先保证企业乙的全体职工每月最低生活费的开支3600元后，逐步偿还转让费（不计息）．根据甲提供的资料有：①这种消费品的进价为每件14元；②该店月销量Q（百件）与销售价格P（元）的关系如图所示；③每月需各种开支2000元．