题目内容
定义方程f(x)=f′(x)的实数根x0叫做函数f(x)的“萌点”,如果函数g(x)=x,h(x)=ln(x+1),φ(x)=cosx(x∈(
,π)的“萌点”分别为a、b、c,则a、b、c的大小关系是 (从小到大排列)
| π |
| 2 |
考点:不等式比较大小,函数的零点与方程根的关系
专题:函数的性质及应用,不等式的解法及应用
分析:由题设中所给的定义,对三个函数所对应的方程进行研究,分别计算求出a,b,c的值或存在的大致范围,再比较出它们的大小即可.
解答:
解:由题意方程f(x)=f'(x)的实数根x0叫做函数f(x)的“萌点”,
对于函数g(x)=x,由于g′(x)=1,由可得x=1,即a=1,
对于函数h(x)=ln(x+1),由于h′(x)=
,可得ln(x+1)=
,分别画出函数y=ln(x+1)和y=
的图象,如图所示
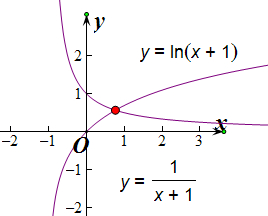
由图象可知0<x<1,
即0<b<1,
对于函数φ(x)=cosx(x∈(
,π),由于φ′(x)=-sinx(x∈(
,π),可得cosx=-sinx,x∈(
,π),
解得x=
,
即c=
>1,
综上b<a<c,
故答案为:b<a<c.
对于函数g(x)=x,由于g′(x)=1,由可得x=1,即a=1,
对于函数h(x)=ln(x+1),由于h′(x)=
| 1 |
| x+1 |
| 1 |
| x+1 |
| 1 |
| x+1 |
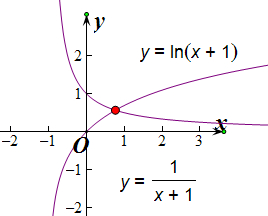
由图象可知0<x<1,
即0<b<1,
对于函数φ(x)=cosx(x∈(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
解得x=
| 3π |
| 4 |
即c=
| 3π |
| 4 |
综上b<a<c,
故答案为:b<a<c.
点评:本题是一个新定义的题,理解定义,分别建立方程解出a,b,c的值或存在范围是解题的关键,本题考查了推理判断的能力,计算能力属于中档题.

练习册系列答案
相关题目
设a,b,c,A,B,C为非零常数,则“ax2+bx+c>0与Ax2+Bx+C>0解集相同”是“
=
=
”的( )
| a |
| A |
| b |
| B |
| c |
| C |
| A、既不充分也不必要条件 |
| B、充分必要条件 |
| C、必要而不充分条件 |
| D、充分而不必要条件 |
设条件p:a≥0;条件q:a2+a≥0,那么p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若P={y|y≥0},Q={x|-
≤x≤
},则P∩Q=( )
| 2 |
| 2 |
A、{0,
| ||||
| B、{(1,1),(-1,-1)} | ||||
C、[0,
| ||||
D、[-
|
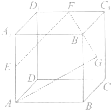 如图,正方体ABCD-A1B1C1D1中,E、F分别是A1A,C1D1的中点,G为正方形BCC1B1的中心,则四边形AEFG在该正方体的各个面的投影不可能是( )
如图,正方体ABCD-A1B1C1D1中,E、F分别是A1A,C1D1的中点,G为正方形BCC1B1的中心,则四边形AEFG在该正方体的各个面的投影不可能是( )
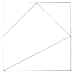

 如图,在60°二面角的棱上有两点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,若AB=4,AC=6,BD=8,则线段CD的长为( )
如图,在60°二面角的棱上有两点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,若AB=4,AC=6,BD=8,则线段CD的长为( )