题目内容
在极坐标系中，求点M (2，
)关于直线θ=
的对称点N的极坐标，并求MN的长．
| π |
| 6 |
| π |
| 4 |
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：把极坐标方程化为直角坐标方程，把点的极坐标化为直角坐标，求得点N的直角坐标，可得线段MN的长，再把点N的直角坐标化为极坐标．
解答：
解：在直角坐标系中，点M（
，1），直线即y=x，
可得点M关于直线的对称点N的直角坐标为（1，
），
∴线段MN的长为
=
=2
．
| 3 |
可得点M关于直线的对称点N的直角坐标为（1，
| 3 |
∴线段MN的长为
(1-
|
8-4
|
2-
|
点评：本题主要考查极坐标方程与直角坐标方程的互化，用点的极坐标刻画点的位置，求出点N的直角坐标，是解题的关键，属于基础题．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
设集合A={1，2，3，4}，B={2，3，5}，则A∩B=（ ）
| A、{5} |
| B、{2，3} |
| C、{2，3，5} |
| D、{1，4，5} |
复数
的共轭复数是（ ）
| 5 |
| 2i-1 |
| A、2i+1 | B、-1-2i |
| C、2i-1 | D、1-2i |
已知0＜α＜
，0＜β＜
，sinα=
，cosβ=
，则cos（α+β）=（ ）
| π |
| 2 |
| π |
| 2 |
| 3 |
| 5 |
| 5 |
| 13 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
函数y=sin（2x+
）的一条对称轴是（ ）
| π |
| 6 |
A、直线x=
| ||
B、直线x=
| ||
C、直线x=
| ||
D、直线x=-
|
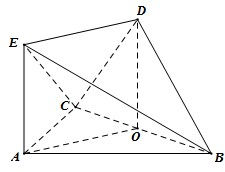如图，边长为2的正三角形△ABC所在平面与等腰直角三角形DBC所在平面相互垂直，已知DB=DC，AE=1，AE⊥平面ABC．