题目内容
某位老师对两个班100名同学进行了是否经常做家务的调查,数据如下表:
如果随机地问这两个班中的一名学生,下面事件发生的概率是多少?
(1)经常做家务;
(2)是二班的同学且不经常做家务.
| 班别 | 经常做家务 | 不经常做家务 | 总数 |
| 一班 | 20 | 32 | 52 |
| 二班 | 25 | 23 | 48 |
| 列总数 | 45 | 55 | 100 |
(1)经常做家务;
(2)是二班的同学且不经常做家务.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)记“抽到经常做家务的学生”为事件A,则事件A包含的基本事件数为45;根据古典概型的概率计算公式可得
(2)记“抽到的同学是二班的同学且不经常做家务”为事件B,则事件B包含的基本事件数为23;根据古典概型的概率计算公式可得
(2)记“抽到的同学是二班的同学且不经常做家务”为事件B,则事件B包含的基本事件数为23;根据古典概型的概率计算公式可得
解答:
解:(1)这是一个古典概型,因为试验的可能结果是有限的,而且等可能性的:100名同学,随机抽到任何一个同学都有相同的可能性,即基本事件总数为100;
记“抽到经常做家务的学生”为事件A,则事件A包含的基本事件数为45;
根据古典概型的概率计算公式可得
P(A)=
=
(2)与(1)相同,随机抽到两个班中任何一名同学都是等可能性的,基本事件总数为100;
记“抽到的同学是二班的同学且不经常做家务”为事件B,则事件B包含的基本事件数为23;
根据古典概型的概率计算公式可得
P(B)=
记“抽到经常做家务的学生”为事件A,则事件A包含的基本事件数为45;
根据古典概型的概率计算公式可得
P(A)=
| 45 |
| 100 |
| 9 |
| 20 |
(2)与(1)相同,随机抽到两个班中任何一名同学都是等可能性的,基本事件总数为100;
记“抽到的同学是二班的同学且不经常做家务”为事件B,则事件B包含的基本事件数为23;
根据古典概型的概率计算公式可得
P(B)=
| 23 |
| 100 |
点评:本题主要考查了古典概型的概率问题,关键是找到基本事件的个数,属于基础题.

练习册系列答案
相关题目
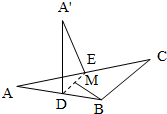 在直角△ABC中,AB=BC=2,D,E分别是AB,AC的中点,将△ADE沿线段DE折起到△A′DE,使平面A′DE⊥平面DBCE,当M是DE的中点时,证明:BM⊥面A′CD.
在直角△ABC中,AB=BC=2,D,E分别是AB,AC的中点,将△ADE沿线段DE折起到△A′DE,使平面A′DE⊥平面DBCE,当M是DE的中点时,证明:BM⊥面A′CD.