题目内容
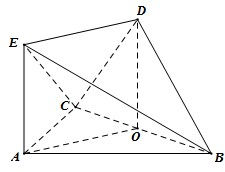 如图,边长为2的正三角形△ABC所在平面与等腰直角三角形DBC所在平面相互垂直,已知DB=DC,AE=1,AE⊥平面ABC.
如图,边长为2的正三角形△ABC所在平面与等腰直角三角形DBC所在平面相互垂直,已知DB=DC,AE=1,AE⊥平面ABC.(Ⅰ)求证:DE∥平面ABC;
(Ⅱ)求证:BD⊥平面CDE;
(Ⅲ)求三棱锥C-BDE的体积.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)取BC的中点O,连接OA,OD,由已知条件推导出AODE为平行四边形,由此能证明DE∥平面ABC.
(Ⅱ)由已知条件推导出AO∥DE,AO⊥BD,ED⊥BD,CD⊥BD,由此能证明BD⊥平面CDE.
(Ⅲ)由AO⊥平面BCD,知AO⊥DE,从而得到DE⊥CD,由此能求出三棱锥C-BDE的体积.
(Ⅱ)由已知条件推导出AO∥DE,AO⊥BD,ED⊥BD,CD⊥BD,由此能证明BD⊥平面CDE.
(Ⅲ)由AO⊥平面BCD,知AO⊥DE,从而得到DE⊥CD,由此能求出三棱锥C-BDE的体积.
解答:
 (Ⅰ)证明:取BC的中点O,连接OA,OD,
(Ⅰ)证明:取BC的中点O,连接OA,OD,
∵△DBC是等腰直角三角形,面ABC⊥面DBC,DO⊥BC,
∴DO⊥面ABC,DO=1,
又∵AE⊥平面ABC,∴AE∥OD,AE=1,
∴四边形AODE为平行四边形,∴AO∥DE,
∵OA?面ABC,DE?面ABC,∴DE∥平面ABC.…4分
(Ⅱ)证明:由(Ⅰ)得AO∥DE,
又AO⊥平面BCD,∴AO⊥BD,∴ED⊥BD,
又∵CD⊥BD,CD∩ED=D,∴BD⊥平面CDE…8分
(Ⅲ)解:∵AO⊥平面BCD,∴AO⊥DE,
∵AO∥DE∴DE⊥平面BCD,∴DE⊥CD,
∴S△EDC=
DE•DC=
×
×
=
,
∴VC-BDE=VB-CDE=
S△CDE•BD=
×
×
=
.…12分.
 (Ⅰ)证明:取BC的中点O,连接OA,OD,
(Ⅰ)证明:取BC的中点O,连接OA,OD,∵△DBC是等腰直角三角形,面ABC⊥面DBC,DO⊥BC,
∴DO⊥面ABC,DO=1,
又∵AE⊥平面ABC,∴AE∥OD,AE=1,
∴四边形AODE为平行四边形,∴AO∥DE,
∵OA?面ABC,DE?面ABC,∴DE∥平面ABC.…4分
(Ⅱ)证明:由(Ⅰ)得AO∥DE,
又AO⊥平面BCD,∴AO⊥BD,∴ED⊥BD,
又∵CD⊥BD,CD∩ED=D,∴BD⊥平面CDE…8分
(Ⅲ)解:∵AO⊥平面BCD,∴AO⊥DE,
∵AO∥DE∴DE⊥平面BCD,∴DE⊥CD,
∴S△EDC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
∴VC-BDE=VB-CDE=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 2 |
| ||
| 3 |
点评:本题综合考察空间线、面的位置关系,体积的计算公式,中等题.解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
把黑、红、白3张纸牌分给甲、乙、丙三人,每人一张,则事件“甲分得红牌”与“乙分得红牌”是( )
| A、对立事件 |
| B、必然事件 |
| C、不可能事件 |
| D、互斥但不对立事件 |
吉安市高二数学竞赛中有一道难题,在30分钟内,学生甲内解决它的概率为
,学生乙能解决它的概率为
,两人在30分钟内独立解决该题,该题得到解决的概率为( )
| 1 |
| 5 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
y=2sin(x+
),x∈[0,
].最大值 为( )
| π |
| 3 |
| π |
| 2 |
| A、1 | ||
B、
| ||
| C、-2 | ||
| D、2 |