题目内容
已知0＜α＜
，0＜β＜
，sinα=
，cosβ=
，则cos（α+β）=（ ）
| π |
| 2 |
| π |
| 2 |
| 3 |
| 5 |
| 5 |
| 13 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
考点：两角和与差的余弦函数
专题：计算题,三角函数的求值
分析：先利用同角三角函数基本关系式求出cosα和sinβ，然后利用两角和的余弦公式展开代入即可求出cos（α+β）．
解答：
解：∵0＜α＜
，sinα=
，
∴cosα=
∵0＜β＜
，cosβ=
，
∴sinβ=
∴cos（α+β）=cosαcosβ-sinαsinβ
=
×
-
×
=-
．
故选：D．
| π |
| 2 |
| 3 |
| 5 |
∴cosα=
| 4 |
| 5 |
∵0＜β＜
| π |
| 2 |
| 5 |
| 13 |
∴sinβ=
| 12 |
| 13 |
∴cos（α+β）=cosαcosβ-sinαsinβ
=
| 4 |
| 5 |
| 5 |
| 13 |
| 3 |
| 5 |
| 12 |
| 13 |
=-
| 16 |
| 65 |
故选：D．
点评：本题考查了同角三角函数基本关系式及两角和的余弦公式，键解题的关键是正确使用公式进行求解．
练习册系列答案
相关题目
设函数f（x）=x+sinπx，则f（
）+f（
）+…+f（
）+f（
）的值为（ ）
| 1 |
| 2014 |
| 2 |
| 2014 |
| 4026 |
| 2014 |
| 4027 |
| 2014 |
| A、4027 | B、2014 |
| C、2013 | D、0 |
若数列{an}的前n项和Sn=n2-1，则a4=（ ）
| A、7 | B、8 | C、9 | D、17 |
吉安市高二数学竞赛中有一道难题，在30分钟内，学生甲内解决它的概率为
，学生乙能解决它的概率为
，两人在30分钟内独立解决该题，该题得到解决的概率为（ ）
| 1 |
| 5 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
离散型随机变量的分布列为：
则x的值为（ ）
| ξ | 0 | 1 | 2 | 3 | ||||||
| P |
|
|
|
x |
A、
| ||
B、
| ||
C、
| ||
D、
|
y=2sin（x+
），x∈[0，
]．最大值 为（ ）
| π |
| 3 |
| π |
| 2 |
| A、1 | ||
B、
| ||
| C、-2 | ||
| D、2 |
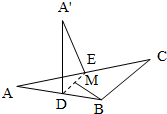在直角△ABC中，AB=BC=2，D，E分别是AB，AC的中点，将△ADE沿线段DE折起到△A′DE，使平面A′DE⊥平面DBCE，当M是DE的中点时，证明：BM⊥面A′CD．