题目内容
已知函数f(x)=ax2+bx+c,不等式f(x)≤0的解集为区间[0,2],且f(x)在区间[0,3]上的最大值为3
(1)求函数f(x)的解析式;
(2)回答下列问题(只需将答案填在横线上,不必写出解题过程)
①已知直线l:x-y+m=0与曲线C:y=f(x)(0≤x≤2).若直线l与曲线段C有且只有一个交点,则m的取值范围是 .
(1)求函数f(x)的解析式;
(2)回答下列问题(只需将答案填在横线上,不必写出解题过程)
①已知直线l:x-y+m=0与曲线C:y=f(x)(0≤x≤2).若直线l与曲线段C有且只有一个交点,则m的取值范围是
考点:二次函数在闭区间上的最值,直线与圆锥曲线的关系
专题:函数的性质及应用,不等式的解法及应用
分析:(1)由不等式f(x)≤0的解集为区间[0,2],得到x=0,x=2是方程ax2+bx+c=0(a>0)的两个根,然后结合根与系数关系得到b=-2a,c=0.即f(x)=ax2-2ax,由
f(x)在区间[0,3]上的最大值为3求得a=1,则函数解析式可求;
(2)由题意画出图形,数形结合得答案.
f(x)在区间[0,3]上的最大值为3求得a=1,则函数解析式可求;
(2)由题意画出图形,数形结合得答案.
解答:
解:(1)∵不等式f(x)≤0的解集为区间[0,2],
∴x=0,x=2是方程ax2+bx+c=0(a>0)的两个根,
则
,即b=-2a,c=0.
∴f(x)=ax2-2ax,对称轴方程为x=1,
∴f(x)在区间[0,3]上的最大值为f(3)=9a-6a=3a=3,即a=1.
∴f(x)=x2-2x;
(2)如图,

由图可知,要使直线l:x-y+m=0与曲线C:y=f(x)(0≤x≤2)有且只有一个交点,则m的取值范围是(-2,0].
故答案为(-2,0].
∴x=0,x=2是方程ax2+bx+c=0(a>0)的两个根,
则
|
∴f(x)=ax2-2ax,对称轴方程为x=1,
∴f(x)在区间[0,3]上的最大值为f(3)=9a-6a=3a=3,即a=1.
∴f(x)=x2-2x;
(2)如图,

由图可知,要使直线l:x-y+m=0与曲线C:y=f(x)(0≤x≤2)有且只有一个交点,则m的取值范围是(-2,0].
故答案为(-2,0].
点评:本题考查了函数解析式的求解及常用方法,考查了二次函数的最值,训练了数形结合的解题思想方法,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
利用数学归纳法证明
+
+
+…+
<1(n∈N*,且n≥2)时,第一步不等式左端是( )
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
A、1+
| ||||||
B、
| ||||||
C、1+
| ||||||
D、
|
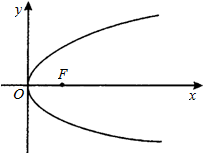 已知抛物线C的顶点在原点,焦点F在x轴上,抛物线上的点A到F的距离为2,且A的横坐标为1.
已知抛物线C的顶点在原点,焦点F在x轴上,抛物线上的点A到F的距离为2,且A的横坐标为1.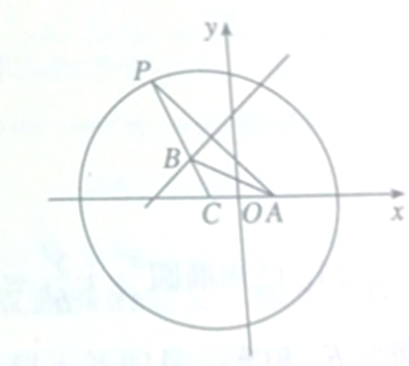 如图,已知点A的坐标为(1,0),点P为圆(x+1)2+y2=16上任意一点,点C为圆心,线段PA的垂直平分线交PC于点B.
如图,已知点A的坐标为(1,0),点P为圆(x+1)2+y2=16上任意一点,点C为圆心,线段PA的垂直平分线交PC于点B.