题目内容
已知α,β为锐角,sinα=
,cos(α-β)=
,求cosβ.
| 8 |
| 17 |
| 21 |
| 29 |
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:由已知数据可得cosα和sin(α-β)的值,而cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β),代值计算可得.
解答:
解:∵α,β为锐角,∴-
<α-β<
,
又∵sinα=
,cos(α-β)=
,
∴cosα=
=
,
∴sin(α-β)=±
=±
,
∴当sin(α-β)=
时,cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β)=
;
当sin(α-β)=-
时,cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β)=
| π |
| 2 |
| π |
| 2 |
又∵sinα=
| 8 |
| 17 |
| 21 |
| 29 |
∴cosα=
| 1-sin2α |
| 15 |
| 17 |
∴sin(α-β)=±
| 1-cos2(α-β) |
| 20 |
| 29 |
∴当sin(α-β)=
| 20 |
| 29 |
| 475 |
| 493 |
当sin(α-β)=-
| 20 |
| 29 |
| 155 |
| 493 |
点评:本题考查两角和与差的三角函数公式,涉及同角三角函数基本关系,属中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
过抛物线y2=2px(p>0)的焦点作直线交抛物线于P,Q两点,若线段PQ中点的横坐标为3,|PQ|=10,则抛物线方程是( )
| A、y2=4x |
| B、y2=2x |
| C、y2=8x |
| D、y2=6x |
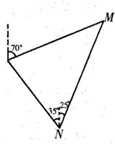 如图,一艘轮船从N处开始按照北偏西35°的方向以每小时30海里的速度航行,灯塔M原来在轮船的北偏东25°方向上,经过30分钟后,灯塔在轮船的北偏东70°方向上,则灯塔M距离N处的海里数为( )
如图,一艘轮船从N处开始按照北偏西35°的方向以每小时30海里的速度航行,灯塔M原来在轮船的北偏东25°方向上,经过30分钟后,灯塔在轮船的北偏东70°方向上,则灯塔M距离N处的海里数为( )A、
| ||||
B、
| ||||
C、30(
| ||||
D、30(
|