题目内容
2.已知无穷数列{an},a1=1,a2=2,对任意n∈N*,有an+2=an,数列{bn}满足bn+1-bn=an(n∈N*),若数列$\{\frac{{{b_{2n}}}}{a_n}\}$中的任意一项都在该数列中重复出现无数次,则满足要求的b1的值为2.分析 依题意数列{an}是周期数咧,则可写出数列{an}的通项,由数列{bn}满足bn+1-bn=an(n∈N*),可推出bn+1-bn=an=$\left\{\begin{array}{l}{1,n为奇数}\\{2,n为偶数}\end{array}\right.$⇒$\frac{{b}_{2}}{{a}_{1}}={b}_{2}$,$\frac{{b}_{4}}{{a}_{2}}=\frac{{b}_{4}}{2}$,$\frac{{b}_{6}}{{a}_{3}}={b}_{6}$,$\frac{{b}_{8}}{{a}_{4}}=\frac{{b}_{8}}{2}$,…要使数列$\{\frac{{{b_{2n}}}}{a_n}\}$中的任意一项都在该数列中重复出现无数次,则b2=b6=b10=…=b2n-1,b4=b8=b12=…=b4n,可得b8=b4=3即可,
解答 解:a1=1,a2=2,对任意n∈N*,有an+2=an,
∴a3=a1=1,a4=a2=2,a5=a3=a1=1,
∴an=$\left\{\begin{array}{l}{1,n为奇数}\\{2,n为偶数}\end{array}\right.$
∴bn+1-bn=an=$\left\{\begin{array}{l}{1,n为奇数}\\{2,n为偶数}\end{array}\right.$,
∴b2n+2-b2n+1=a2n+1=1,b2n+1-b2n=a2n=2,
∴b2n+2-b2n=3,b2n+1-b2n-1=3
∴b3-b1=b5-b3=…=b2n+1-b2n-1=3,
b4-b2=b6-b4=b8-b6=…=b2n-b2n-2=3,b2-b1=1,
$\frac{{b}_{2}}{{a}_{1}}={b}_{2}$,$\frac{{b}_{4}}{{a}_{2}}=\frac{{b}_{4}}{2}$,$\frac{{b}_{6}}{{a}_{3}}={b}_{6}$,$\frac{{b}_{8}}{{a}_{4}}=\frac{{b}_{8}}{2}$,…,$\frac{{b}_{4n-2}}{{a}_{2n-1}}$=b4n-2,$\frac{{b}_{4n}}{{a}_{2n}}=\frac{{b}_{4n}}{2}$,
∵数列$\{\frac{{{b_{2n}}}}{a_n}\}$中的任意一项都在该数列中重复出现无数次,
∴b2=b6=b10=…=b4n-2,
b4=b8=b12=…=b4n,
解得b8=b4=3,
b2=3,∵b2-b1=1,∴b1=2,
故答案为:2
点评 本题考查了数列的推理与证明,属于难题.

| A. | 4 | B. | 8 | C. | 9 | D. | 10 |
| A. | (-1,1] | B. | [-1,1] | C. | (-∞,1] | D. | [-1,+∞) |
| A. | [-1,+∞) | B. | (-1,+∞) | C. | $({-1,-\frac{1}{3}})∪({-\frac{1}{3},+∞})$ | D. | $({-1,-\frac{1}{3}})∪({-\frac{1}{3},0}]$ |
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -1 | D. | 1 |
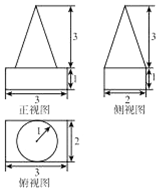
| A. | 6+π | B. | 4+π | C. | 3+π | D. | 2+π |
 发改委10月19日印发了《中国足球中长期发展规划(2016-2050年)重点任务分工》通知,其中“十三五”校园足球普及行动排名第三,为了调查重庆八中高一高二两个年级对改政策的落实情况,在每个年级随机选取20名足球爱好者,记录改政策发布后他们周平均增加的足球运动时间(单位:h),所得数据如下:
发改委10月19日印发了《中国足球中长期发展规划(2016-2050年)重点任务分工》通知,其中“十三五”校园足球普及行动排名第三,为了调查重庆八中高一高二两个年级对改政策的落实情况,在每个年级随机选取20名足球爱好者,记录改政策发布后他们周平均增加的足球运动时间(单位:h),所得数据如下: