题目内容
18.已知当x∈[0,1]时,函数y=(mx-1)2 的图象与y=$\sqrt{x}$+m的图象有且只有一个交点,则正实数m的取值范围是( )| A. | (0,1]∪[2$\sqrt{3}$,+∞) | B. | (0,1]∪[3,+∞) | C. | (0,$\sqrt{2}$)∪[2$\sqrt{3}$,+∞) | D. | (0,$\sqrt{2}$]∪[3,+∞) |
分析 根据题意,由二次函数的性质分析可得:y=(mx-1)2 为二次函数,在区间(0,$\frac{1}{m}$)为减函数,($\frac{1}{m}$,+∞)为增函数,分2种情况讨论:①、当0<m≤1时,有$\frac{1}{m}$≥1,②、当m>1时,有$\frac{1}{m}$<1,结合图象分析两个函数的单调性与值域,可得m的取值范围,综合可得答案.
解答 解:根据题意,由于m为正数,y=(mx-1)2 为二次函数,在区间(0,$\frac{1}{m}$)为减函数,($\frac{1}{m}$,+∞)为增函数,
函数y=$\sqrt{x}$+m为增函数,
分2种情况讨论:
①、当0<m≤1时,有$\frac{1}{m}$≥1,
在区间[0,1]上,y=(mx-1)2 为减函数,且其值域为[(m-1)2,1],
函数y=$\sqrt{x}$+m为增函数,其值域为[m,1+m],
此时两个函数的图象有1个交点,符合题意;
②、当m>1时,有$\frac{1}{m}$<1,
y=(mx-1)2 在区间(0,$\frac{1}{m}$)为减函数,($\frac{1}{m}$,1)为增函数,
函数y=$\sqrt{x}$+m为增函数,其值域为[m,1+m],
若两个函数的图象有1个交点,则有(m-1)2≥1+m,
解可得m≤0或m≥3,
又由m为正数,则m≥3;
综合可得:m的取值范围是(0,1]∪[3,+∞);
故选:B.
点评 本题考查函数图象的交点问题,涉及函数单调性的应用,关键是确定实数m的分类讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )
| A. | 12种 | B. | 18种 | C. | 24种 | D. | 36种 |
10.设变量x,y满足约束条件$\left\{\begin{array}{l}{2x+y≥0}\\{x+2y-2≥0}\\{x≤0}\\{y≤3}\end{array}\right.$,则目标函数z=x+y的最大值为( )
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 3 |
6.若回归直线的斜率$\widehatb∈(0,+∞)$,则相关系数r的取值范围为( )
| A. | (0,1] | B. | [-1,0) | C. | 0 | D. | 无法确定 |
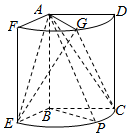 如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点.
如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点.