题目内容
已知奇函数y=f(x),在(0,+∞)上满足2f(x+1)=f(x),且当0<x<1时,f(x)=3x,则不等式f(x)≥x的解集为 .
考点:函数的图象,抽象函数及其应用
专题:函数的性质及应用
分析:在(0,+∞)上满足2f(x+1)=f(x),故f(x)=
f(x-1),由此推出f(0)=f(1)=f(2)=0,同理f(3)=0等等,
当1<x<2时,易推f(x)=
×3x-1,以此类推,可得x在(0,+∞)上的其它区间上的函数表达式,
在直角坐标系内画出函数在(0,+∞)上的图象,再根据函数为奇函数,图象关于原点对称,画出函数在(0,+∞)上的图象,结合图象得出不等式的解.
| 1 |
| 2 |
当1<x<2时,易推f(x)=
| 1 |
| 2 |
在直角坐标系内画出函数在(0,+∞)上的图象,再根据函数为奇函数,图象关于原点对称,画出函数在(0,+∞)上的图象,结合图象得出不等式的解.
解答:
解:在(0,+∞)上满足2f(x+1)=f(x),∴f(x)=
f(x-1),
∵f(x)为奇函数,f(0)=0,∴f(1)=
f(0)=0,f(2)=
f(1)=0,同理f(3)=0等等,
而当1<x<2时,f(x)=
f(x-1),而0<x-1<1,
∵当0<x<1时,f(x)=3x,∴f(x)=
f(x-1)=
×3x-1,
∴当1<x<2时,f(x)=
×3x-1,以此类推,可得x在(0,+∞)上的其它区间上的函数表达式,
在直角坐标系内画出函数在(0,+∞)上的图象,再根据函数为奇函数,图象关于原点对称,画出函数在(0,+∞)上的图象,如下图:
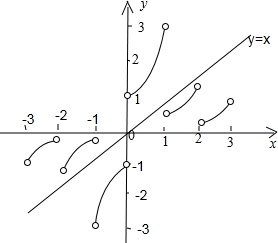
从图象知:
要使不等式f(x)≥x成立,x应满足:x∈(-∞,-1]∪[0,1),
故答案为:(-∞,-1]∪[0,1)
| 1 |
| 2 |
∵f(x)为奇函数,f(0)=0,∴f(1)=
| 1 |
| 2 |
| 1 |
| 2 |
而当1<x<2时,f(x)=
| 1 |
| 2 |
∵当0<x<1时,f(x)=3x,∴f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
∴当1<x<2时,f(x)=
| 1 |
| 2 |
在直角坐标系内画出函数在(0,+∞)上的图象,再根据函数为奇函数,图象关于原点对称,画出函数在(0,+∞)上的图象,如下图:

从图象知:
要使不等式f(x)≥x成立,x应满足:x∈(-∞,-1]∪[0,1),
故答案为:(-∞,-1]∪[0,1)
点评:本题主要考查函数的性质,由函数的奇偶性得出整个图象,数形结合得出自变量的范围,要注意函数在端点处的函数值.

练习册系列答案
相关题目
已知a,b∈R+且a≠b,x=
,y=
则x,y的大小关系是( )
| ||||
| 2 |
| a+b, |
| A、x<y | B、x>y |
| C、x=y | D、视a,b的值而定 |
用0,1,2,3四个数字组成没有重复数字的四位奇数有( )个.
| A、4 | B、8 | C、24 | D、64 |
若对于满足不等式组
的任意实数x,y,都有x+y≥a恒成立,则实数a的取值范围是( )
|
| A、(-∞,-2] |
| B、(-∞,0] |
| C、(-∞,2] |
| D、[-2,2] |
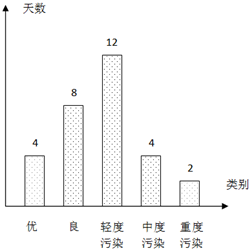 经过对某市空气质量指数进行一个月(30天)监测,获得数据后得到条形图统计图:
经过对某市空气质量指数进行一个月(30天)监测,获得数据后得到条形图统计图: