题目内容
14.已知椭圆的中心在原点,焦点在坐标轴上,它的长轴长为短轴长的3倍,且此椭圆经过点A(3,1),求这个椭圆的标准方程.分析 先设出椭圆的标准形式,再由长轴是短轴长的3倍,结合过点A(3,1),列出关于a,b的方程组,解此方程组即可求得a或b的值,进而可求得椭圆的方程.
解答 解:由题设可知,椭圆的方程是标准方程.a=3b.
(1)当焦点在x轴上时,设椭圆方程为$\frac{{x}^{2}}{9{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1
代入点A(3,1),可得$\frac{9}{9{b}^{2}}$+$\frac{1}{{b}^{2}}$=1,∴b2=2
此时椭圆的方程是$\frac{{x}^{2}}{18}+\frac{{y}^{2}}{2}=1$;
(2)当焦点在y轴上时,设椭圆方程为$\frac{{y}^{2}}{9{b}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1.
代入点A(3,1),可得$\frac{1}{9{b}^{2}}$+$\frac{9}{{b}^{2}}$=1,∴b2=$\frac{82}{9}$
此时椭圆的方程是$\frac{{y}^{2}}{82}+\frac{{x}^{2}}{\frac{82}{9}}$=1.
综上,所求椭圆方程为$\frac{{x}^{2}}{18}+\frac{{y}^{2}}{2}=1$或$\frac{{y}^{2}}{82}+\frac{{x}^{2}}{\frac{82}{9}}$=1.
点评 本题主要考查椭圆的基本性质的运用等基础知识,考查运算求解能力,考查分类讨论思想、方程思想.属于基础题.

练习册系列答案
相关题目
2.设f(x)=$\frac{1+x}{1-x}$,又记f1(x)=f(x),fk+1(x)=f(fk(x)),k=1,2,…,则f2008(x)=( )
| A. | $\frac{1+x}{1-x}$ | B. | $\frac{x-1}{x+1}$ | C. | x | D. | -$\frac{1}{x}$ |
 (3)请认真阅读下列程序框图:已知程序框图
(3)请认真阅读下列程序框图:已知程序框图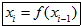 中的函数关系式为$f(x)=\frac{4x-2}{x+1}$,程序框图中的D为函数f(x)的定义域,把此程序框图中所输出的数xi组成一个数列{xn}
中的函数关系式为$f(x)=\frac{4x-2}{x+1}$,程序框图中的D为函数f(x)的定义域,把此程序框图中所输出的数xi组成一个数列{xn}