题目内容
16．设复数$z=1+\frac{1}{i^3}$，则z的共轭复数是（ ）| A． | 1 | B． | 1+i | C． | -1+i | D． | 1-i |
分析 利用复数的代数形式的乘除运算，解得z=1-i，由此能求出z的共轭复数．
解答 解：z=1+$\frac{1}{{i}^{3}}$=1+$\frac{i}{{i}^{4}}$=1+i，
∴z的共轭复数是1-i，
故选：D
点评 本题考查复数的代数形式的乘除运算，是基础题．解题时要认真审题，仔细解答．注意熟练掌握共轭复数的概念．
练习册系列答案
相关题目
6．设集合A={x|x-3＜0}，B={y|y=2x，x∈[1，2]}，则A∩B=（ ）
| A． | ∅ | B． | （1，3） | C． | [2，3） | D． | （1，4] |
7．已知函数f（x）=$\left\{\begin{array}{l}{f（x-5）\\;x＞2}\\{a{e}^{x}\\;x≤2}\end{array}\right.$，若f（2017）=e2，则a=（ ）
| A． | 2 | B． | 1 | C． | -1 | D． | -2 |
4．直线l：ax+$\frac{1}{a}$y-1=0与x，y轴的交点分别为A，B，直线l与圆O：x2+y2=1的交点为C，D．给出下列命题：p：?a＞0，S△AOB=$\frac{1}{2}$，q：?a＞0，|AB|＜|CD|．则下面命题正确的是（ ）
| A． | p∧q | B． | ￢p∧￢q | C． | p∧￢q | D． | ￢p∧q |
11．已知函数$f（x）=\left\{\begin{array}{l}{log_{\frac{1}{3}}}x，x＞0\\{2^x}，x≤0\end{array}\right.$，若$f（a）＞\frac{1}{2}$，则实数a的取值范围是（ ）
| A． | $（{0，\frac{{\sqrt{3}}}{3}}）$ | B． | （-1，0] | C． | $（{-1，\frac{{\sqrt{3}}}{3}}）$ | D． | $（{-1，0}）∪（{0，\frac{{\sqrt{3}}}{3}}）$ |
8．
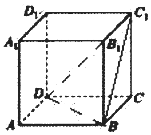在正方体ABCD-A1B1C1D1中，过点A作平面α平行平面BDC1，平面α与平面A1ADD1交于直线m，平面α与平面A1ABB1交于直线n，则直线m与直线n所成的角为（ ）
在正方体ABCD-A1B1C1D1中，过点A作平面α平行平面BDC1，平面α与平面A1ADD1交于直线m，平面α与平面A1ABB1交于直线n，则直线m与直线n所成的角为（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
5．如图所示是用模拟方法估计圆周率π值的程序框图，m表示估计结果，则图中空白处应填入（ ）
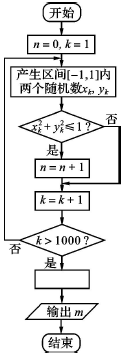
| A． | $m=\frac{n}{4000}$ | B． | $m=\frac{n}{1000}$ | C． | $m=\frac{n}{500}$ | D． | $m=\frac{n}{250}$ |