ĢāÄæÄŚČŻ
11£®ŅŃÖŖŗÆŹż$f£Øx£©=\left\{\begin{array}{l}{log_{\frac{1}{3}}}x£¬x£¾0\\{2^x}£¬x”Ü0\end{array}\right.$£¬Čō$f£Øa£©£¾\frac{1}{2}$£¬ŌņŹµŹżaµÄȔֵ·¶Ī§ŹĒ£Ø””””£©| A£® | $£Ø{0£¬\frac{{\sqrt{3}}}{3}}£©$ | B£® | £Ø-1£¬0] | C£® | $£Ø{-1£¬\frac{{\sqrt{3}}}{3}}£©$ | D£® | $£Ø{-1£¬0}£©”Č£Ø{0£¬\frac{{\sqrt{3}}}{3}}£©$ |
·ÖĪö ĄūÓĆ·Ö¶ĪŗÆŹż£¬½įŗĻŅŃÖŖĢõ¼ž£¬ĮŠ³ö²»µČŹ½×飬×Ŗ»ÆĒó½ā¼“æÉ£®
½ā“š ½ā£ŗÓÉĢāŅā£¬µĆ$\left\{\begin{array}{l}{log_{\frac{1}{3}}}x£¾\frac{1}{2}\\ x£¾0\end{array}\right.$»ņ$\left\{\begin{array}{l}{2^x}£¾\frac{1}{2}\\ x”Ü0\end{array}\right.$£¬½āµĆ$0£¼a£¼\frac{{\sqrt{3}}}{3}$»ņ-1£¼a”Ü0£¬
¼“ŹµŹżaµÄȔֵ·¶Ī§ĪŖ$£Ø{-1£¬\frac{{\sqrt{3}}}{3}}£©$£¬
¹ŹŃ”C£®
µćĘĄ ±¾Ģāæ¼²é·Ö¶ĪŗÆŹżµÄÓ¦ÓĆ£¬²»µČŹ½×éµÄĒó½ā£¬æ¼²é¼ĘĖćÄÜĮ¦£®

Į·Ļ°²įĻµĮŠ“š°ø
Ļą¹ŲĢāÄæ
2£®ŅŃÖŖŗÆŹż$f£Øx£©=sin£Ø¦Ųx+¦Õ£©£Ø¦Ų£¾0£¬|¦Õ|£¼\frac{¦Š}{2}£©$µÄ×īŠ”ÕżÖÜĘŚĪŖ¦Š£¬f£Øx£©µÄĶ¼ĻóĻņ×óĘ½ŅĘ$\frac{¦Š}{3}$øöµ„Ī»ŗó¹ŲÓŚÖ±Ļßx=0¶Ō³Ę£¬Ōņ$f£Øx+\frac{¦Š}{12}£©+f£Øx-\frac{¦Š}{6}£©$µÄµ„µ÷µŻŌöĒų¼äĪŖ£Ø””””£©
| A£® | [k¦Š-$\frac{11¦Š}{24}$£¬k¦Š+$\frac{¦Š}{24}$]£Øk”ŹZ£© | B£® | $[k¦Š+\frac{3¦Š}{8}£¬k¦Š+\frac{7¦Š}{8}]£Øk”ŹZ£©$ | ||
| C£® | $[2k¦Š-\frac{¦Š}{4}£¬2k¦Š+\frac{3¦Š}{4}]£Øk”ŹZ£©$ | D£® | $[2k¦Š+\frac{3¦Š}{4}£¬2k¦Š+\frac{7¦Š}{4}]£Øk”ŹZ£©$ |
19£®ŅŃÖŖČ«¼ÆU=R£¬¼ÆŗĻA={x|x2+x-6£¾0}£¬B={y|y=2x-1£¬x”Ü2}£¬Ōņ£Ø∁UA£©”ÉB=£Ø””””£©
| A£® | [-3£¬3] | B£® | [-1£¬2] | C£® | [-3£¬2] | D£® | £Ø-1£¬2] |
6£®ŅŃÖŖĖ«ĒśĻß$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1£Øa£¾0£¬b£¾0£©µÄ×óÓŅ½¹µć·Ö±šĪŖF1£Ø-c£¬0£©£¬F2£Øc£¬0£©£¬ŅŌĻ߶ĪF1F2ĪŖÖ±¾¶µÄŌ²ÓėĖ«ĒśĻßŌŚµŚ¶žĻóĻŽµÄ½»µćĪŖP£¬ČōÖ±ĻßPF2ÓėŌ²E£ŗ£Øx-$\frac{c}{2}$£©2+y2=$\frac{{b}^{2}}{16}$ĻąĒŠ£¬ŌņĖ«ĒśĻߵĽ„½üĻß·½³ĢŹĒ£Ø””””£©
| A£® | y=”Ąx | B£® | y=”Ą2x | C£® | y=”Ą$\sqrt{3}$x | D£® | y=”Ą$\sqrt{2}$x |
16£®Éčø“Źż$z=1+\frac{1}{i^3}$£¬ŌņzµÄ¹²éīø“ŹżŹĒ£Ø””””£©
| A£® | 1 | B£® | 1+i | C£® | -1+i | D£® | 1-i |
20£®ŅŃÖŖ$f£Øx£©=\left\{\begin{array}{l}£Ø3-a£©x-a£¬x£¼1\\{log_a}x£¬x”Ż1\end{array}\right.$ŹĒ£Ø-”Ž£¬+”Ž£©ÉĻµÄŌöŗÆŹż£¬ÄĒĆ“ŹµŹżaµÄȔֵ·¶Ī§ŹĒ£Ø””””£©
| A£® | £Ø1£¬+”Ž£© | B£® | £Ø1£¬3£© | C£® | £Ø0£¬1£©”Č£Ø1£¬3£© | D£® | $[\frac{3}{2}£¬3£©$ |
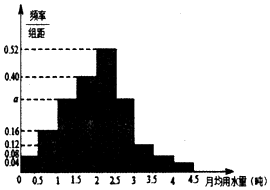 Ė®ŹĒµŲĒņÉĻ±¦¹óµÄ׏Ō“£¬ÓÉÓŚ¼Ūøń±Č½Ļ±ćŅĖŌŚŗܶą²»Č±Ė®µÄ³ĒŹŠ¾ÓĆń¾³£ĪŽ½ŚÖʵď¹ÓĆĖ®×ŹŌ“Ōģ³ÉŃĻÖŲµÄ׏Ō“ĄĖ·Ń£®Ä³ŹŠÕžø®ĪŖĮĖĢį³«µĶĢ¼»·±£µÄÉś»īĄķÄī¹ÄĄų¾ÓĆń½ŚŌ¼ÓĆĖ®£¬¼Ę»®µ÷Õū¾ÓĆńÉś»īÓĆĖ®ŹÕ·Ń·½°ø£¬ÄāČ·¶ØŅ»øöŗĻĄķµÄŌĀÓĆĖ®Įæ±ź×¼x£Ø¶Ö£©£¬Ņ»Ī»¾ÓĆńµÄŌĀÓĆĖ®Įæ²»³¬¹żxµÄ²æ·Ö°“Ę½¼ŪŹÕ·Ń£¬³¬³öxµÄ²æ·Ö°“Ņé¼ŪŹÕ·Ń£®ĪŖĮĖĮĖ½ā¾ÓĆńÓĆĖ®Ēéæö£¬Ķعż³éŃł£¬»ńµĆĮĖÄ³Äź100Ī»¾ÓĆńĆæČĖµÄŌĀ¾łÓĆĖ®Įæ£Øµ„Ī»£ŗ¶Ö£©£¬½«Źż¾Ż°“ÕÕ[0£¬0.5£©£¬[0.5£¬1£©£¬[1£¬1.5£©£¬”£¬[4£¬4.5£©·Ö³É9×飬ÖĘ³ÉĮĖČēĶ¼ĖłŹ¾µÄʵĀŹ·Ö²¼Ö±·½Ķ¼£®
Ė®ŹĒµŲĒņÉĻ±¦¹óµÄ׏Ō“£¬ÓÉÓŚ¼Ūøń±Č½Ļ±ćŅĖŌŚŗܶą²»Č±Ė®µÄ³ĒŹŠ¾ÓĆń¾³£ĪŽ½ŚÖʵď¹ÓĆĖ®×ŹŌ“Ōģ³ÉŃĻÖŲµÄ׏Ō“ĄĖ·Ń£®Ä³ŹŠÕžø®ĪŖĮĖĢį³«µĶĢ¼»·±£µÄÉś»īĄķÄī¹ÄĄų¾ÓĆń½ŚŌ¼ÓĆĖ®£¬¼Ę»®µ÷Õū¾ÓĆńÉś»īÓĆĖ®ŹÕ·Ń·½°ø£¬ÄāČ·¶ØŅ»øöŗĻĄķµÄŌĀÓĆĖ®Įæ±ź×¼x£Ø¶Ö£©£¬Ņ»Ī»¾ÓĆńµÄŌĀÓĆĖ®Įæ²»³¬¹żxµÄ²æ·Ö°“Ę½¼ŪŹÕ·Ń£¬³¬³öxµÄ²æ·Ö°“Ņé¼ŪŹÕ·Ń£®ĪŖĮĖĮĖ½ā¾ÓĆńÓĆĖ®Ēéæö£¬Ķعż³éŃł£¬»ńµĆĮĖÄ³Äź100Ī»¾ÓĆńĆæČĖµÄŌĀ¾łÓĆĖ®Įæ£Øµ„Ī»£ŗ¶Ö£©£¬½«Źż¾Ż°“ÕÕ[0£¬0.5£©£¬[0.5£¬1£©£¬[1£¬1.5£©£¬”£¬[4£¬4.5£©·Ö³É9×飬ÖĘ³ÉĮĖČēĶ¼ĖłŹ¾µÄʵĀŹ·Ö²¼Ö±·½Ķ¼£®