题目内容
4.直线l:ax+$\frac{1}{a}$y-1=0与x,y轴的交点分别为A,B,直线l与圆O:x2+y2=1的交点为C,D.给出下列命题:p:?a>0,S△AOB=$\frac{1}{2}$,q:?a>0,|AB|<|CD|.则下面命题正确的是( )| A. | p∧q | B. | ¬p∧¬q | C. | p∧¬q | D. | ¬p∧q |
分析 利用已知条件求出三角形的面积,判断p的真假;求出|AB|与|CD|的差,判断大小,推出真假,然后判断选项即可.
解答 解:直线l:ax+$\frac{1}{a}$y-1=0与x,y轴的交点分别为A($\frac{1}{a}$,0),B(0,a),
S△AOB=$\frac{1}{2}$$•a•\frac{1}{a}$=$\frac{1}{2}$,
∴p是真命题;
直线l:ax+$\frac{1}{a}$y-1=0与x,y轴的交点分别为A($\frac{1}{a}$,0),B(0,a),
|AB|=$\sqrt{{a}^{2}+\frac{1}{{a}^{2}}}$,
直线l与圆O:x2+y2=1的交点为C,D.d=$\sqrt{\frac{1}{{a}^{2}+\frac{1}{{a}^{2}}}}$,
|CD|=2$\sqrt{1-\frac{1}{{a}^{2}+\frac{1}{{a}^{2}}}}$,|AB|2-|CD|2=${a}^{2}+\frac{1}{{a}^{2}}+\frac{4}{{a}^{2}+\frac{1}{{a}^{2}}}-4$≥0,
∴|AB|≥|CD|,
所以q假,
故选:C.
点评 本题考查命题的真假的判断与应用,考查直线与圆的位置关系的应用,直线的特征,考查转化思想以及计算能力.

练习册系列答案
相关题目
14.按照图中的程序框图执行,若M处条件是k>16,则输出结果为( )
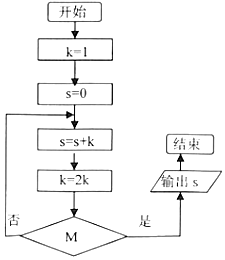

| A. | 15 | B. | 16 | C. | 31 | D. | 32 |
12.已知抛物线C:y2=4x的焦点为F,准线为l,过点F的直线交抛物线于A,B两点(A在第一象限),过点A作准线l的垂线,垂足为E,若∠AFE=60°,则△AFE的面积为( )
| A. | $4\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
19.已知全集U=R,集合A={x|x2+x-6>0},B={y|y=2x-1,x≤2},则(∁UA)∩B=( )
| A. | [-3,3] | B. | [-1,2] | C. | [-3,2] | D. | (-1,2] |
9.在等差数列{an}中,已知a3+a8=6,则3a2+a16的值为( )
| A. | 24 | B. | 18 | C. | 16 | D. | 12 |
16.设复数$z=1+\frac{1}{i^3}$,则z的共轭复数是( )
| A. | 1 | B. | 1+i | C. | -1+i | D. | 1-i |
13.在等差数列{an}中,a2=3,a5+a7=10,则a1+a10=( )
| A. | 9 | B. | 9.5 | C. | 10 | D. | 11 |
13.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线与圆${(x-\sqrt{3})^2}+{(y-1)^2}=1$相切,则此双曲线的离心率为( )
| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |