题目内容
6.设集合A={x|x-3<0},B={y|y=2x,x∈[1,2]},则A∩B=( )| A. | ∅ | B. | (1,3) | C. | [2,3) | D. | (1,4] |
分析 求出A中不等式的解集确定出A,求出B中y的范围确定出B,找出A与B的交集即可.
解答 解:由A中不等式解得:x<3,即A=(-∞,3),
由B中y=2x,x∈[1,2],得到2≤y≤4,即B=[2,4],
则A∩B=[2,3),
故选:C.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
17.复数z=$\frac{2{i}^{2}+4}{i+1}$的虚部为( )
| A. | -3 | B. | -1 | C. | 1 | D. | 2 |
14.按照图中的程序框图执行,若M处条件是k>16,则输出结果为( )
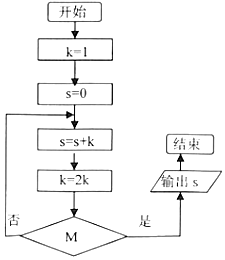

| A. | 15 | B. | 16 | C. | 31 | D. | 32 |
11.函数y=$\frac{1}{x}$+$\frac{1}{3-x}$(0<x<3)的最小值为( )
| A. | 1 | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | 2 |
18.若复数z 满足z(1+i)=-2i(i为虚数单位),$\overline z$是z 的共轭复数,则$\overline z$•z=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 1 |
16.设复数$z=1+\frac{1}{i^3}$,则z的共轭复数是( )
| A. | 1 | B. | 1+i | C. | -1+i | D. | 1-i |