题目内容
在△ABC中，a，b，c分别是角A，B，C的对边，若a2-c2=2b，且sinB=6cosAsinC，则b的值为 ．
考点：正弦定理,余弦定理
专题：解三角形
分析：通过正弦定理以及余弦定理化简已知表达式，然后求出的b值．
解答：
解：在△ABC中，由sinB=6cosAsinC可得 sin（A+C）=sinAcosC+cosAsinC=6cosAsinC，
化简可得sinAcosC=5cosAsinC，∴a•
=5c•
，即 2b2=3a2-3c2．
再由a2-c2=2b，可得 2b2=3•2b，∴b=3，
故答案为：3．
化简可得sinAcosC=5cosAsinC，∴a•
| a2+b2-c2 |
| 2ab |
| b2+c2-a2 |
| 2bc |
再由a2-c2=2b，可得 2b2=3•2b，∴b=3，
故答案为：3．
点评：本题主要考查诱导公式、正弦定理以及余弦定理的应用，考查计算能力，属于基础题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
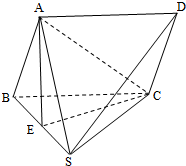如图，在四棱锥S-ABCD中，底面ABCD是平行四边形，侧SBC是正三角形，点E是SB的中点，且AE⊥平面ABC．
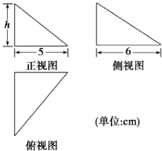图中的三个直角三角形是一个体积为20cm3的几何体的三视图，则h=