题目内容
设a为函数f(x)=x2+2α
+α2-6α+13,设t=
.
(1)求t的取值范围并将f(x)表示为关于t的函数g(t);
(2)求函数g(t)的最大值m,用a表示.
| 1-x2 |
| 1-x2 |
(1)求t的取值范围并将f(x)表示为关于t的函数g(t);
(2)求函数g(t)的最大值m,用a表示.
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用
分析:(1)由t=
可得0≤t≤1;从而求g(t)=1-t2+2at+α2-6α+13=-(t-a)2+2a2-6a+14,t∈[0,1];
(2)由g(t)=-(t-a)2+2a2-6a+14,t∈[0,1]讨论a以确定函数的最大值,从而写出最大值.
| 1-x2 |
(2)由g(t)=-(t-a)2+2a2-6a+14,t∈[0,1]讨论a以确定函数的最大值,从而写出最大值.
解答:
解:(1)t=
,则0≤t≤1;
x2=1-t2;
则g(t)=1-t2+2at+α2-6α+13
=-(t-a)2+2a2-6a+14,t∈[0,1];
(2)g(t)=-(t-a)2+2a2-6a+14,t∈[0,1];
当a≤0时,gmax(t)=g(0)=a2-6a+14,
当0<a<1时,gmax(t)=g(a)=2a2-6a+14,
当a≥1时,gmax(t)=g(1)=α2-4α+13.
故gmax(t)=
.
| 1-x2 |
x2=1-t2;
则g(t)=1-t2+2at+α2-6α+13
=-(t-a)2+2a2-6a+14,t∈[0,1];
(2)g(t)=-(t-a)2+2a2-6a+14,t∈[0,1];
当a≤0时,gmax(t)=g(0)=a2-6a+14,
当0<a<1时,gmax(t)=g(a)=2a2-6a+14,
当a≥1时,gmax(t)=g(1)=α2-4α+13.
故gmax(t)=
|
点评:本题考查了换元法的应用及分段函数的应用,属于中档题.

练习册系列答案
相关题目
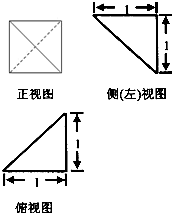
一个四面体的三视图如图所示,则该四面体的四个面中最大的面积是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( )
| A、至多有一次中靶 |
| B、两次都中靶 |
| C、只有一次中靶 |
| D、两次都不中靶 |