题目内容
在直角坐标系xOy中,曲线C1的点均在圆C2:x2+(y-5)2=9外,且对C1上任意一点M,M到直线y=-2的距离等于该点与圆C2上点的距离的最小值.
(Ⅰ)求曲线C1的方程;
(Ⅱ)设P为直线y=-4上的一点,过P作圆C2的两条切线,分别与曲线C1相交于点A,B和C,D,证明:四点A,B,C,D的横坐标之积为定值.
(Ⅰ)求曲线C1的方程;
(Ⅱ)设P为直线y=-4上的一点,过P作圆C2的两条切线,分别与曲线C1相交于点A,B和C,D,证明:四点A,B,C,D的横坐标之积为定值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设点M(x,y),由已知条件推导出
=y+5,由此能求出曲线C1的方程.
(Ⅱ)当点P在直线y=-4上运动时,设P(x0,-4),切线方程为kx-y-kx0-4=0,所以(x02-9)k2+18x0k+72=0,设过P所作的两条切线PA,PC的斜率分别为k1,k2,则k1+k2=-
,k1k2=-
,由
,得x2-20k1x+20(k1x0+4)=0,设四点A、B、C、D的横向联合坐标分别是x1,x2,x3,x4,则x1x2=20(k1x0+4),x3x4=20(k2x0+4),由此能证明四点A,B,C,D的横坐标之积为定值.
| x2+(y-5)2 |
(Ⅱ)当点P在直线y=-4上运动时,设P(x0,-4),切线方程为kx-y-kx0-4=0,所以(x02-9)k2+18x0k+72=0,设过P所作的两条切线PA,PC的斜率分别为k1,k2,则k1+k2=-
| 18x0 |
| x02-9 |
| 72 |
| x02-9 |
|
解答:
解:(Ⅰ)设点M(x,y),
由已知得|y+2|=
-3,
且圆C2上的点位于直线y=-2的上方,
于是y+2>0,
∴
=y+5,
化简得曲线C1的方程为:x2=20y.
(Ⅱ)证明:当点P在直线y=-4上运动时,设P(x0,-4),
由题意知x0≠±3,过P且于圆C2相切的直线的斜率存在,
每条切线都与抛物线有两个交点,
切线方程为y+4=k(x-x0),即kx-y-kx0-4=0,
∴
=3,
整理,得(x02-9)k2+18x0k+72=0,①
设过P所作的两条切线PA,PC的斜率分别为k1,k2,
则k1,k2是方程①的两个实根,
∴k1+k2=-
,k1k2=-
,②
由
,得x2-20k1x+20(k1x0+4)=0,③
设四点A、B、C、D的横向联合坐标分别是x1,x2,x3,x4,
则x1,x2是方程③的两个实根,
∴x1x2=20(k1x0+4),④
同理,x3x4=20(k2x0+4),⑤
由②④⑤三式得:
x1x2x3x4=400(k1x0+4)(k2x0+4)
=400[k1k2x02+4x0(k1+k2)+16]
=400(
-4x0•
+16)
=400×16=6400.
∴当点P在直线y=-4上运动时,四点A、B、C、D的横坐标之积为定值6400.
由已知得|y+2|=
| x2+(y-5)2 |
且圆C2上的点位于直线y=-2的上方,
于是y+2>0,
∴
| x2+(y-5)2 |
化简得曲线C1的方程为:x2=20y.
(Ⅱ)证明:当点P在直线y=-4上运动时,设P(x0,-4),
由题意知x0≠±3,过P且于圆C2相切的直线的斜率存在,
每条切线都与抛物线有两个交点,
切线方程为y+4=k(x-x0),即kx-y-kx0-4=0,
∴
| |-5-kx0-4| | ||
|
整理,得(x02-9)k2+18x0k+72=0,①
设过P所作的两条切线PA,PC的斜率分别为k1,k2,
则k1,k2是方程①的两个实根,
∴k1+k2=-
| 18x0 |
| x02-9 |
| 72 |
| x02-9 |
由
|
设四点A、B、C、D的横向联合坐标分别是x1,x2,x3,x4,
则x1,x2是方程③的两个实根,
∴x1x2=20(k1x0+4),④
同理,x3x4=20(k2x0+4),⑤
由②④⑤三式得:
x1x2x3x4=400(k1x0+4)(k2x0+4)
=400[k1k2x02+4x0(k1+k2)+16]
=400(
| 72x02 |
| x02-9 |
| 18x0 |
| x02-9 |
=400×16=6400.
∴当点P在直线y=-4上运动时,四点A、B、C、D的横坐标之积为定值6400.
点评:本题考查曲线方程的求法,考查四点的横坐标之积为定值的证明,解题时要认真审题,注意直线方程、韦达定理等知识点的合理运用.

练习册系列答案
相关题目
下列命题或等式正确的是( )
| A、若f(x)是奇函数,则f(0)=0 | ||
B、∫
| ||
| C、函数f(x)=cos2x是周期为π的减函数 | ||
| D、若a∈R,则“a2<a”是“a>0”的必要条件 |
函数f(x)=Asin(ωx+ϕ)+b的图象如图所示,则S=f(0)+f(1)+…+f(2014)等于( )
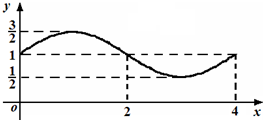

| A、0 | ||
B、
| ||
C、
| ||
D、
|
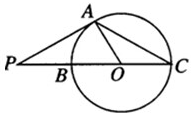 如图,已知P是圆O外一点,PA为圆O的切线,A为切点.割线PBC经过圆心O,若PA=3
如图,已知P是圆O外一点,PA为圆O的切线,A为切点.割线PBC经过圆心O,若PA=3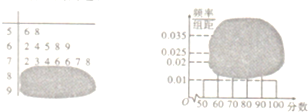 某高校自主招生面试成绩的茎叶图和频率分布直方图均受到不同程度的破坏,其可见部分信息如图所示,据此解答下列问题;
某高校自主招生面试成绩的茎叶图和频率分布直方图均受到不同程度的破坏,其可见部分信息如图所示,据此解答下列问题; 如图,PC切⊙O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,已知⊙O的半径为3,PA=2,则OE=
如图,PC切⊙O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,已知⊙O的半径为3,PA=2,则OE=