题目内容
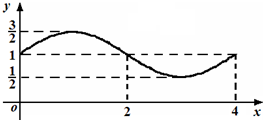
函数f（x）=Asin（ωx+ϕ）+b的图象如图所示，则S=f（0）+f（1）+…+f（2014）等于（ ）
| A、0 | ||
B、
| ||
C、
| ||
D、
|
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：先根据图象观察得出4为函数的一个周期，以及f（0），f（1），f（2），f（3），f（4）的值，并能计算出在一个周期内四个函数值的和，最后看从f（1）到f（2014）有多少个周期，余数是多少，最后计算结果即可．
解答：
解：依图可知函数f（x）的周期为4，
f（0）=1，f（1）=
，f（2）=1，f（3）=
，f（4）=1，
f（1）+f（2）+f（3）+f（4）=4
∵
=503余2，
∴S=f（0）+503×4+
+1=
，
故选D．
f（0）=1，f（1）=
| 3 |
| 2 |
| 1 |
| 2 |
f（1）+f（2）+f（3）+f（4）=4
∵
| 2014 |
| 4 |
∴S=f（0）+503×4+
| 3 |
| 2 |
| 4031 |
| 2 |
故选D．
点评：本题主要考查了三角函数的周期问题．利用函数的周期性，先对一个周期进行计算，再看有多少个周期即可．
练习册系列答案
相关题目
执行如图所示的程序框图，则输出的S的值为（ ）
| A、-7 | B、8 | C、-9 | D、-5 |
（
）2014=（ ）
| 1+i |
| 1-i |
| A、i | B、-1 | C、1 | D、-i |
已知向量
=（sin（α+
），1），
=（1，cosα-
），若
⊥
，则sin（α+
）等于（ ）
| a |
| π |
| 6 |
| b |
| 3 |
| a |
| b |
| π |
| 3 |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
函数f（x）=sin（ωx+
）（ω＞0）的图象与x轴的交点的横坐标构成一个公差为
的等差数列，要得到函数g（x）=sinωx的图象，只需将f（x）的图象（ ）
| π |
| 6 |
| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
抛物线y=8x2的焦点到准线的距离是（ ）
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |