题目内容
下列命题或等式正确的是（ ）
| A、若f（x）是奇函数，则f（0）=0 | ||
B、∫
| ||
| C、函数f（x）=cos2x是周期为π的减函数 | ||
| D、若a∈R，则“a2＜a”是“a＞0”的必要条件 |
考点：微积分基本定理,必要条件
专题：导数的概念及应用
分析：本题需根据奇函数的性质，微积分基本定理，余弦函数的性质，必要条件分别加以判别，得出正确选项．
解答：
解：选项A：若f（x）是奇函数，则f（0）=0，需要考虑其定义域，故不正确．
选项B：∫
（-x+1）dx=(-
x2+x)
=-
×22+2=0，故正确．
选项C：余弦函数的单调性不一致，故不正确．
选项D：可以举反例，例如：令a=1，则12=1，故不正确．
故选：B．
选项B：∫
2 0 |
| 1 |
| 2 |
| | | 2 0 |
| 1 |
| 2 |
选项C：余弦函数的单调性不一致，故不正确．
选项D：可以举反例，例如：令a=1，则12=1，故不正确．
故选：B．
点评：本题考查了奇函数的性质，微积分基本定理，余弦函数的性质，必要条件基础知识，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
如图，在边长为a的正方形内有不规则图形Ω．向正方形内随机撒豆子，若撒在图形Ω内和正方形内的豆子数分别为m，n，则图形Ω面积的估计值为执行如图所示的程序框图，则输出的S的值为（ ）
| A、-7 | B、8 | C、-9 | D、-5 |
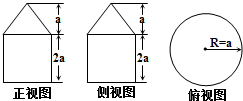已知一个几何体的三视图如图所示，则此几何体的侧面积是（ ）| A、4πa2 | ||
| B、5πa2 | ||
C、（4+
| ||
D、（5+
|
已知集合M=（-2，-1，0，1，2，3}，N={x|y=
}，则M∩N为（ ）
| ln(3-x) | ||
|
| A、{0，1，2} |
| B、{-1，0，1，2} |
| C、{-2，-1，0} |
| D、{0，1，2，3} |
执行如图所示的程序框图，输出的S值为-4时，则输入的S0的值为（ ）
| A、7 | B、8 | C、9 | D、10 |
（
）2014=（ ）
| 1+i |
| 1-i |
| A、i | B、-1 | C、1 | D、-i |
已知向量
=（sin（α+
），1），
=（1，cosα-
），若
⊥
，则sin（α+
）等于（ ）
| a |
| π |
| 6 |
| b |
| 3 |
| a |
| b |
| π |
| 3 |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|