题目内容
8.已知正方形ABCD的边长为2,E为CD的中点,则$\overrightarrow{AC}•\overrightarrow{BE}$=2.分析 方法一:根据两个向量的加减法的法则,以及其几何意义,可得要求的式子,再根据两个向量垂直的性质,运算求得结果.
方法二:以A为原点,以AB为x轴,以AD为y轴建立直角坐标系,利用坐标的运算即可求出.
解答 解:(解法一)$\overrightarrow{AC}•\overrightarrow{BE}=(\overrightarrow{AB}+\overrightarrow{AD})•(\overrightarrow{BC}+\overrightarrow{CE})=(\overrightarrow{AB}+\overrightarrow{AD})•(\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB})$=${\overrightarrow{AD}^2}-\frac{1}{2}{\overrightarrow{AB}^2}=4-2=2$.
(解法二)以A为原点,以AB为x轴,以AD为y轴建立直角坐标系,$\overrightarrow{AC}=(2,2)$,$\overrightarrow{BE}=(-1,2)$,$\overrightarrow{AC}•\overrightarrow{BE}=2$.
故答案为:2.
点评 本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量垂直的性质,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
19.设$\overrightarrow{a}$,$\overrightarrow{b}$是两个非零向量,则下列哪个描述是正确的( )
| A. | 若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$|,则$\overrightarrow{a}$$⊥\overrightarrow{b}$ | B. | 若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| | ||
| C. | 若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$|,则存在实数λ使得$\overrightarrow{a}$=$λ\overrightarrow{b}$ | D. | 若存在实数λ使得$\overrightarrow{a}$=$λ\overrightarrow{b}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| |
13.已知直角梯形ABCD,AD∥BC,∠BAD=90°.AD=2,BC=1,P是腰AB上的动点,则$|\overrightarrow{PC}+\overrightarrow{PD}|$的最小值为3.
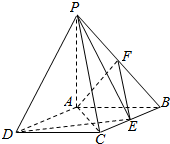 如图:四棱锥P-ABCD中,底面ABCD是平行四边形,且AC=BD,PA⊥底面ABCD,PA=AB=1,$BC=\sqrt{3}$,点F是PB的中点,点E在边BC上移动.
如图:四棱锥P-ABCD中,底面ABCD是平行四边形,且AC=BD,PA⊥底面ABCD,PA=AB=1,$BC=\sqrt{3}$,点F是PB的中点,点E在边BC上移动.