题目内容
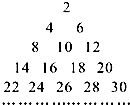把正偶数数列{2n}的数按上小下大，左小右大的原则排列成如图“三角形”所示的数表，设aij（i，j∈N*）是位于这个三角形数表中从上往下数第i行，从左往右数第j个数，若amn=2014，则m+n=考点：归纳推理
专题：探究型,推理和证明
分析：由题义正偶数an为等差数列，由图摆放找每一行所放的数，及每一行的数字总数与本数列的每一项的关系即可发现规律
解答：
解：由图可知，第一行放1个偶数，第二行放2个偶数，第3行放3个偶数…
又因为amn=2014指图中摆放的第m行第n列，
所以先求第m行的最后一个偶数（该偶数小于2014且是最接近的，并且还能成为每一行最后一个数字的）应为第44行的最后一偶数是1980，
接着可以断定2014应位于45行故m=45，
又第45行的第一个偶数为1982，利用等差数列的任意两项之间关系可知2014应出在该行的第17列故n=17，
所以m+n=62．
故答案为：62．
又因为amn=2014指图中摆放的第m行第n列，
所以先求第m行的最后一个偶数（该偶数小于2014且是最接近的，并且还能成为每一行最后一个数字的）应为第44行的最后一偶数是1980，
接着可以断定2014应位于45行故m=45，
又第45行的第一个偶数为1982，利用等差数列的任意两项之间关系可知2014应出在该行的第17列故n=17，
所以m+n=62．
故答案为：62．
点评：此题重点考查了等差数列的通项公式，任意两项之间及项与项数之间的关系，另外还考查了学生的观察与分析能力．
练习册系列答案
相关题目