题目内容
已知向量
=（2，-1，3），
=（-4，2，x），则使“
⊥
”和“
∥
”的x之和为 ．
| a |
| b |
| a |
| b |
| a |
| b |
考点：向量的数量积判断向量的共线与垂直
专题：空间向量及应用
分析：当
⊥
时，
•
=2×（-4）+（-1）×2+3x=0，当
∥
时，
=
=
，由此能求出使“
⊥
”和“
∥
”的x之和．
| a |
| b |
| a |
| b |
| a |
| b |
| -4 |
| 2 |
| 2 |
| -1 |
| x |
| 3 |
| a |
| b |
| a |
| b |
解答：
解：∵向量
=（2，-1，3），
=（-4，2，x），
∴当
⊥
时，
•
=2×（-4）+（-1）×2+3x=0，解得x=
，
当
∥
时，
=
=
，解得x=-6．
∴使“
⊥
”和“
∥
”的x之和为：
+(-6)=-
．
故答案为：-
．
| a |
| b |
∴当
| a |
| b |
| a |
| b |
| 10 |
| 3 |
当
| a |
| b |
| -4 |
| 2 |
| 2 |
| -1 |
| x |
| 3 |
∴使“
| a |
| b |
| a |
| b |
| 10 |
| 3 |
| 8 |
| 3 |
故答案为：-
| 8 |
| 3 |
点评：本题考查向量垂直和向量平行的性质的应用，解题时要认真审题，是基础题．
练习册系列答案
相关题目
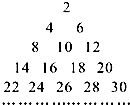把正偶数数列{2n}的数按上小下大，左小右大的原则排列成如图“三角形”所示的数表，设aij（i，j∈N*）是位于这个三角形数表中从上往下数第i行，从左往右数第j个数，若amn=2014，则m+n=
函数f（x）的图象如图所示，下列数值排序正确的是（ ）
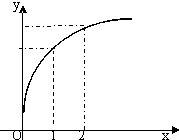
| A、0＜f′（1）＜f′（2）＜f（2）-f（1） |
| B、0＜f′（2）＜f（2）-f（1）＜f′（1） |
| C、0＜f′（2）＜f′（1）＜f（2）-f（1） |
| D、0＜f（2）-f（1）＜f′（1）＜f′（2） |