题目内容
在正方体AC1中,面对角线A1B与对角面BB1D1D所成的角的大小为 .
考点:直线与平面所成的角
专题:空间角
分析:连接A1C1交B1D1于O,连接OB,说明∠ABO为A1B与平面BB1D1D所成的角,然后求解即可.
解答:
 解:连接A1C1交B1D1于O,连接OB,
解:连接A1C1交B1D1于O,连接OB,
因为B1D1⊥A1C1,A1C1⊥BB1,所以A1C1⊥平面BB1D1D,
所以∠ABO为A1B与平面BB1D1D所成的角,
设正方体棱长为1,所以A1O=
,A1B=
,
则sin∠A1BO=
=
,
故∠ABO=30°.
故答案为:30°.
 解:连接A1C1交B1D1于O,连接OB,
解:连接A1C1交B1D1于O,连接OB,因为B1D1⊥A1C1,A1C1⊥BB1,所以A1C1⊥平面BB1D1D,
所以∠ABO为A1B与平面BB1D1D所成的角,
设正方体棱长为1,所以A1O=
| ||
| 2 |
| 2 |
则sin∠A1BO=
| ||||
|
| 1 |
| 2 |
故∠ABO=30°.
故答案为:30°.
点评:本题考查直线与平面所成角的求法,找出直线与平面所成角是解题的关键,考查计算能力.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
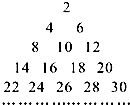 把正偶数数列{2n}的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表,设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行,从左往右数第j个数,若amn=2014,则m+n=
把正偶数数列{2n}的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表,设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行,从左往右数第j个数,若amn=2014,则m+n=