题目内容
16．（3x+1）n的二项展开式中，二项式系数和为256，则在展开式中x2的系数是324．分析 由题意利用二项式系数的性质求得n=9，再根据二项展开式的通项公式求得展开式中x2的系数．
解答 解：由题意可得2n=256，∴n=9，在（3x+1）n =（3x+1）9 的二项展开式中，
x2的系数是${C}_{9}^{7}$•（3x）2•1=324，
故答案为：324．
点评 本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目
6．已知三棱锥O-ABC，OA，OB，OC两两垂直，且OA=OB=$\sqrt{2}$，OC=1，P是△ABC上任意一点，设OP与平面ABC所成角为x，OP=y，则y关于x的函数关系图象为（ ）
| A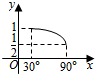． |  | B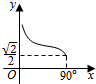． |  | C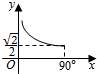． |  | D． |  |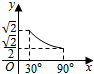
4．已知sin（$\frac{π}{3}$+a）=$\frac{12}{13}$，a∈（$\frac{π}{6}$，$\frac{2π}{3}$），则cosα的值为 （ ）
| A． | $\frac{12\sqrt{3}-5}{13}$ | B． | $\frac{12\sqrt{3}-5}{26}$ | C． | $\frac{12\sqrt{3}+5}{13}$ | D． | $\frac{12\sqrt{3}+5}{26}$ |
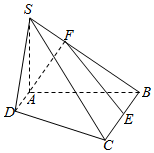如图，在四棱锥S-ABCD中，SA⊥平面ABCD，底面ABCD为直角梯形，AD∥BC，∠BAD=90°，且AB=4，SA=3．
3．已知i是虚数单位，若复数（a+i）（2-i）是纯虚数，则实数a等于（ ）
| A． | 2 | B． | $\frac{1}{2}$ | C． | -$\frac{1}{2}$ | D． | -2 |