题目内容
13.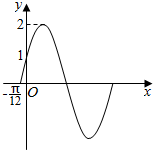 能否由下列图象唯一地确定函数y=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的解析式?如果能.求出它的解析式;如果不能,请你加一个条件.确定它的解析式.
能否由下列图象唯一地确定函数y=Asin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的解析式?如果能.求出它的解析式;如果不能,请你加一个条件.确定它的解析式.
分析 根据三角函数的图象确实A,ω和φ的值即可得到结论.
解答 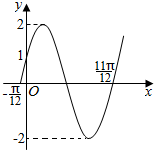 解:由图象知A=2,f(0)=1,无法确定其他条件.
解:由图象知A=2,f(0)=1,无法确定其他条件.
增加一个条件如图:
T=$\frac{2π}{ω}$=$\frac{11π}{12}-(-\frac{π}{12})$=π,可得:ω=2,
∵由点($\frac{11π}{12}$,0)在函数图象上,可得:2sin(2×$\frac{11π}{12}$+φ)=0;
∴2×$\frac{11π}{12}$+φ=kπ,k∈Z,解得:φ=kπ-$\frac{11π}{6}$,k∈Z,
∵0<φ<$\frac{π}{2}$
∴解得:φ=$\frac{π}{6}$.
∴函数解析式为:y=2sin(2x+$\frac{π}{6}$).
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,注意条件0<φ<$\frac{π}{2}$的应用,求出A,ω和φ的值是解决本题的关键.

练习册系列答案
相关题目
4.已知sin($\frac{π}{3}$+a)=$\frac{12}{13}$,a∈($\frac{π}{6}$,$\frac{2π}{3}$),则cosα的值为 ( )
| A. | $\frac{12\sqrt{3}-5}{13}$ | B. | $\frac{12\sqrt{3}-5}{26}$ | C. | $\frac{12\sqrt{3}+5}{13}$ | D. | $\frac{12\sqrt{3}+5}{26}$ |
18.空间中A,B,C,D,E五点不共面,已知A,B,C,D在同一平面内,点B,C,D,E在同一平面内,那么B,C,D三点( )
| A. | 一定构成三角形 | B. | 一定共线 | C. | 不一定共线 | D. | 与A,E共面 |
3.已知i是虚数单位,若复数(a+i)(2-i)是纯虚数,则实数a等于( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |
1.已知直线x+ay-1=0是圆C:x2+y2-4x-2y+1=0的对称轴,过点A(-4,a)作圆C的一条切线,切点为B,则|AB|=( )
| A. | 2 | B. | 6 | C. | 4$\sqrt{2}$ | D. | 2$\sqrt{10}$ |