题目内容
对于任意实数x,不等式|x+2|+|x-2|≥a恒成立.
(1)求a的取值范围;
(2)当a取最大值时,求f(x)=
的单调区间.
(1)求a的取值范围;
(2)当a取最大值时,求f(x)=
-x2-
|
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)利用绝对值不等式的几何意义可求得|x+2|+|x-2|≥4,从而可得a的取值范围;
(2)令g(x)=-x2-2x+3=-(x+1)2+4,由g(x)≥0及二次函数的单调性,复合函数的单调性可求得f(x)=
的单调区间.
(2)令g(x)=-x2-2x+3=-(x+1)2+4,由g(x)≥0及二次函数的单调性,复合函数的单调性可求得f(x)=
-x2-
|
解答:
解:(1)∵|x+2|+|x-2|≥|(x+2)+(2-x)|=4,对于任意实数x,不等式|x+2|+|x-2|≥a恒成立,
∴a≤4;
(2)∵a的最大值为4,
∴f(x)=
,
令g(x)=-x2-2x+3=-(x+1)2+4,其对称轴方程为x=-1;
由g(x)≥0,得-3≤x≤1,
∴g(x)=-x2-2x+3在区间[-3,-1]单调递增,在区间[-1,1]单调递减,
由复合函数的单调性知,f(x)=
在区间[-3,-1]单调递增,在区间[-1,1]单调递减.
即f(x)=
的增区间为[-3,-1],减区间为[-1,1].
∴a≤4;
(2)∵a的最大值为4,
∴f(x)=
| -x2-2x+3 |
令g(x)=-x2-2x+3=-(x+1)2+4,其对称轴方程为x=-1;
由g(x)≥0,得-3≤x≤1,
∴g(x)=-x2-2x+3在区间[-3,-1]单调递增,在区间[-1,1]单调递减,
由复合函数的单调性知,f(x)=
-x2-
|
即f(x)=
-x2-
|
点评:本题考查绝对值不等式的解法,考查复合函数的单调性,属于中档题.

练习册系列答案
相关题目
从5名同学中选3人参加某项会议,则选法种数为( )
| A、15 | B、10 | C、20 | D、60 |
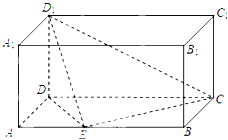 在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB上一点,且不为中点.
在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB上一点,且不为中点.