题目内容
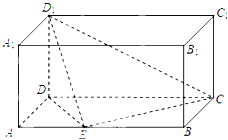 在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB上一点,且不为中点.
在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是棱AB上一点,且不为中点.(1)证明:D1E⊥A1D;
(2)证明:平面D1DE不可能与平面D1BC垂直.
考点:平面与平面垂直的判定,直线与平面垂直的性质
专题:证明题,空间位置关系与距离
分析:(1)建立坐标系,设AE=λEB,求出
=(1,
,-1),
=(-1,0,-1),证明
•
=0,可得D1E⊥A1D;
(2)利用反证法证明平面D1DE不可能与平面D1BC垂直.
| D1E |
| 2λ |
| 1-λ |
| A1D |
| D1E |
| A1D |
(2)利用反证法证明平面D1DE不可能与平面D1BC垂直.
解答:
 (1)证明:建立如图所示的坐标系,则D(0,0,0),A(1,0,0),B(1,2,0),C(0,2,0),A1(1,0,1),B1(1,2,1),C1(0,2,1),D1(0,0,1),
(1)证明:建立如图所示的坐标系,则D(0,0,0),A(1,0,0),B(1,2,0),C(0,2,0),A1(1,0,1),B1(1,2,1),C1(0,2,1),D1(0,0,1),
设AE=λEB,则E(1,
,0),
∴
=(1,
,-1),
=(-1,0,-1),
∴
•
=0,
∴D1E⊥A1D;
(2)∵D1D⊥平面ABCD,∴设平面D1DE的法向量为
=(x,y,0).
∵
=(1,
,-1),∴平面D1DE的一个法向量为
=(
,-1,0),
同理平面D1BC的法向量为
=(2-
,1,2),
由
•
=0可得λ=1,
∴E是棱AB的中点,与题设矛盾,
∴平面D1DE不可能与平面D1BC垂直.
 (1)证明:建立如图所示的坐标系,则D(0,0,0),A(1,0,0),B(1,2,0),C(0,2,0),A1(1,0,1),B1(1,2,1),C1(0,2,1),D1(0,0,1),
(1)证明:建立如图所示的坐标系,则D(0,0,0),A(1,0,0),B(1,2,0),C(0,2,0),A1(1,0,1),B1(1,2,1),C1(0,2,1),D1(0,0,1),设AE=λEB,则E(1,
| 2λ |
| 1-λ |
∴
| D1E |
| 2λ |
| 1-λ |
| A1D |
∴
| D1E |
| A1D |
∴D1E⊥A1D;
(2)∵D1D⊥平面ABCD,∴设平面D1DE的法向量为
| m |
∵
| DE |
| 2λ |
| 1+λ |
| m |
| 2λ |
| 1+λ |
同理平面D1BC的法向量为
| n |
| 2λ |
| 1-λ |
由
| m |
| n |
∴E是棱AB的中点,与题设矛盾,
∴平面D1DE不可能与平面D1BC垂直.
点评:本题考查线线、线面垂直,考查向量方法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
等差数列8,5,2,…的第20项是( )
| A、68 | B、65 |
| C、-46 | D、-49 |
